En digital størrelseskomparator er et kombinationskredsløb, der sammenligner to digitale eller binære tal for at finde ud af, om det ene binære tal er lig med, mindre end eller større end det andet binære tal. Vi designer logisk set et kredsløb, hvor vi vil have to indgange, en for A og en anden for B, og have tre udgangsterminaler, en for A > B-tilstand, en for A = B-tilstand og en for A < B-tilstand.
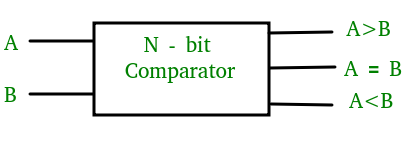
1-bits størrelseskomparator –
En komparator, der bruges til at sammenligne to bits, kaldes en enkeltbitskomparator. Den består af to indgange til hver to enkeltbits tal og tre udgange til at generere mindre end, lig med og større end mellem to binære tal.
Sandhedstabellen for en 1-bit komparator er angivet nedenfor:
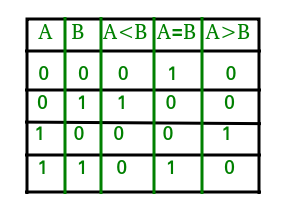
Der kan ud fra ovenstående sandhedstabel udtrykkes logiske udtryk for hver udgang på følgende måde:
A>B: AB'A<B: A'BA=B: A'B' + AB
Fra ovenstående udtryk kan vi udlede følgende formel:

Ved hjælp af disse boolske udtryk kan vi implementere et logisk kredsløb for denne komparator som angivet nedenfor:
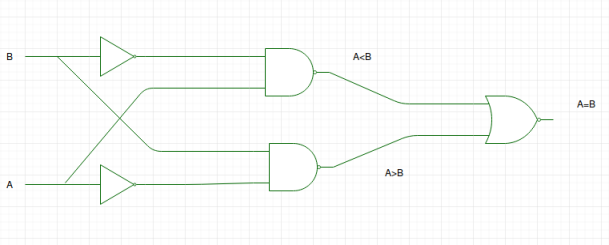
Logikdiagrammet er forkert
2-Bit Magnitude Komparator –
En komparator, der bruges til at sammenligne to binære tal med hver to bits, kaldes en 2-bit Magnitude komparator. Den består af fire indgange og tre udgange til at generere mindre end, lig med og større end mellem to binære tal.
Sandhedstabellen for en 2-bit komparator er angivet nedenfor:
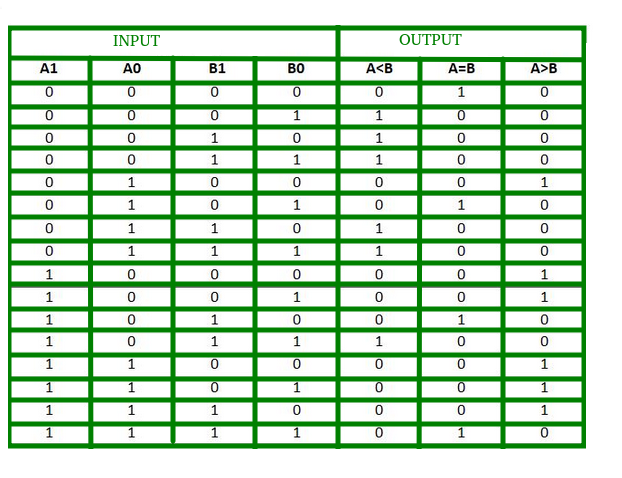
Fra ovenstående sandhedstabel kan K-map for hver udgang tegnes som følger:



Af ovenstående K-map kan logiske udtryk for hver udgang udtrykkes som følger:
A>B:A1B1' + A0B1'B0' + A1A0B0'A=B: A1'A0'B1'B0' + A1'A0B1'B0 + A1A0B1B0 + A1A0'B1B0' : A1'B1' (A0'B0' + A0B0) + A1B1 (A0B0 + A0'B0') : (A0B0 + A0'B0') (A1B1 + A1'B1') : (A0 Ex-Nor B0) (A1 Ex-Nor B1)A<B:A1'B1 + A0'B1B0 + A1'A0'B0
Ved hjælp af disse boolske udtryk kan vi implementere et logisk kredsløb for denne komparator som angivet nedenfor:
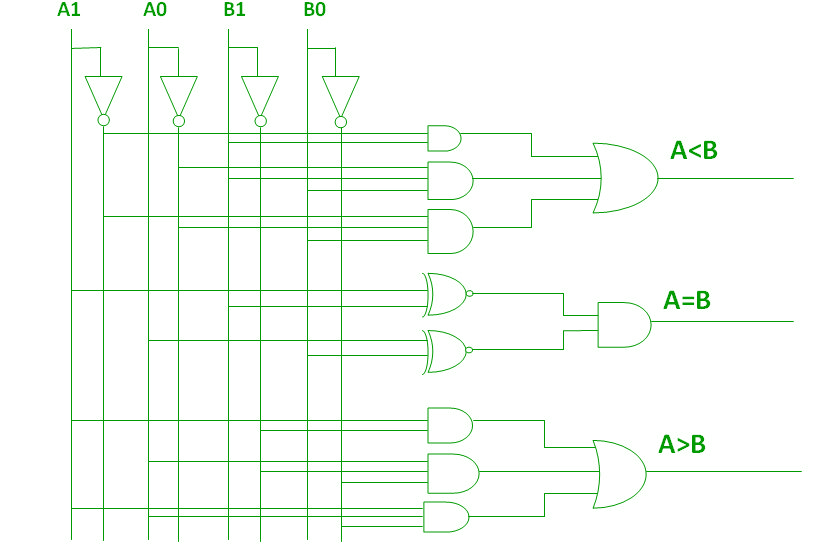
4-bit størrelseskomparator –
En komparator, der anvendes til at sammenligne to binære tal med hver fire bits, kaldes en 4-bit størrelseskomparator. Den består af otte indgange til hver to tal på fire bit og tre udgange til at generere mindre end, lig med og større end mellem to binære tal.
I en 4-bit komparator kan betingelsen A>B være mulig i følgende fire tilfælde:
- Hvis A3 = 1 og B3 = 0
- Hvis A3 = B3 og A2 = 1 og B2 = 0
- Hvis A3 = B3 og A2 = 1 og B2 = 0
- Hvis A3 = B3, A2 = B2 og A1 = 1 og B1 = 0
- Hvis A3 = B3, A2 = B2, A1 = B1 og A0 = 1 og B0 = 0
Sådan kan betingelsen for A<B være mulig i de følgende fire tilfælde:
- Hvis A3 = 0 og B3 = 1
- Hvis A3 = B3 og A2 = 0 og B2 = 1
- Hvis A3 = B3 og A2 = 0 og B2 = 1
- Hvis A3 = B3, A2 = B2 og A1 = 0 og B1 = 1
- Hvis A3 = B3, A2 = B2, A1 = B1 og A0 = 0 og B0 = 1
Betingelsen A=B er kun mulig, når alle de enkelte bits i et tal er nøjagtigt sammenfaldende med de tilsvarende bits i et andet tal.
Fra ovenstående udsagn kan logiske udtryk for hver udgang udtrykkes som følger:
AA, 831331 r: (A3 EioNor 33)A2132′ a (A3 Ex-Nor 133) (A2 Ex-Nor 132)A131′ a (A3 Ex-Nor 33) (A2 ENor132) (Al Ex-Nor 31)A01301
,13: A3’03 a (A3 Ex-Nor 33)A211:12 a (A3 Ex-Nor 83) (A2 Ex-Nor 132)Ar131 a (A3 Ex-Nor 33) (A2 Ex-Nor32) (Al Ex-Nor 131)A0N30
A=B: (A3 Ex-Nor B3) (A2 Ex-Nor 82) (Al Ex-Nor BI) (AO Ex-Nor BO)
Ved hjælp af disse boolske udtryk kan vi implementere et logisk kredsløb for denne komparator som angivet nedenfor:
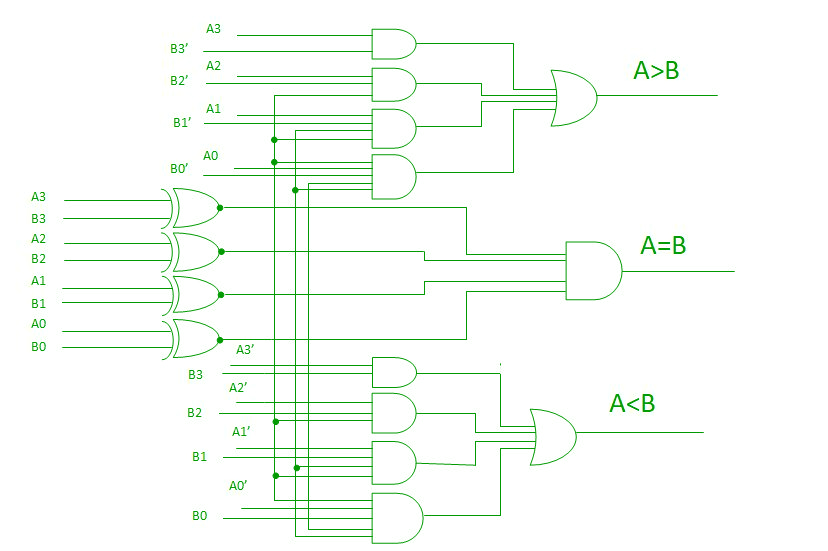
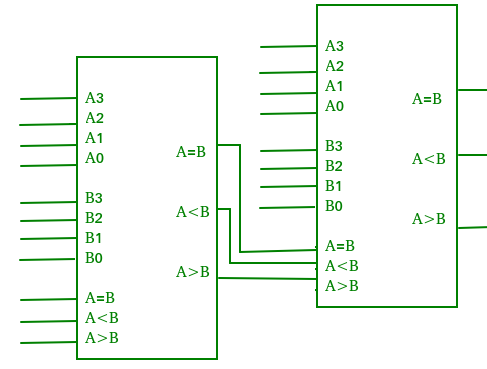
Kaskadekomparator –
En komparator, der udfører sammenligningsoperationen på mere end fire bit ved at kaskadere to eller flere 4-bit komparatorer, kaldes kaskadekomparator. Når to komparatorer skal kaskaderes, forbindes udgangene fra komparatoren af lavere orden med de tilsvarende indgange fra komparatoren af højere orden.