Postet den 29. november 2018 af Maximilian Siebert
Heterogenitet er ikke noget at være bange for, det betyder blot, at der er variabilitet i dine data. Så hvis man samler forskellige undersøgelser for at analysere dem eller lave en metaanalyse, så er det klart, at der vil blive fundet forskelle. Det modsatte af heterogenitet er homogenitet, hvilket betyder, at alle undersøgelser viser den samme effekt.
Det er vigtigt at bemærke, at der findes forskellige typer af heterogenitet:
- Klinisk: Forskelle i deltagere, interventioner eller resultater
- Metodologisk: Forskelle i undersøgelsesdesign, risiko for bias
- Statistisk: Variation i interventionseffekter eller resultater
Vi er interesserede i disse forskelle, fordi de kan indikere, at vores intervention måske ikke virker på samme måde, hver gang den anvendes. Ved at undersøge disse forskelle kan man nå frem til en langt større forståelse af, hvilke faktorer der påvirker interventionen, og hvilket resultat man kan forvente næste gang interventionen implementeres.
Selv om klinisk og metodologisk heterogenitet er vigtig, vil denne blog fokusere på statistisk heterogenitet.
Hvordan man identificerer og måler heterogenitet
Eyeball test
I dit forest plot skal du kigge på overlappende konfidensintervaller, snarere end på hvilken side dine effektestimater er. Om resultaterne ligger på begge sider af linjen for ingen effekt påvirker måske ikke din vurdering af, om der er heterogenitet, men det kan påvirke din vurdering af, om heterogeniteten har betydning.
Med dette i tankerne kan du se på nedenstående graf og beslutte, hvilket plot der er mest homogent.
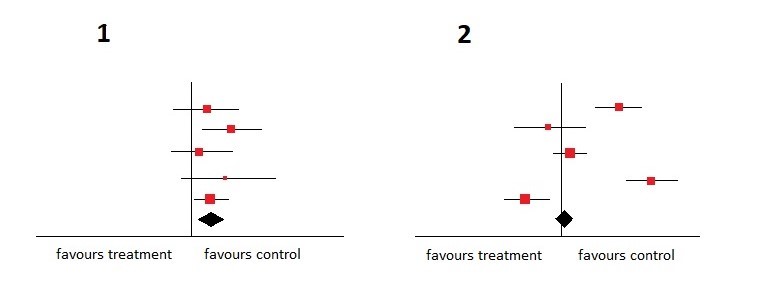
Det mest homogene er naturligvis plot nummer 1 . Konfidensintervallerne overlapper alle sammen, og derudover er alle studierne til fordel for kontrolinterventionen.
For de mennesker, der elsker at måle ting i stedet for bare at se dem i øjnene, skal du ikke være bekymret, der er stadig nogle statistiske metoder, der kan hjælpe dig med at gribe begrebet heterogenitet.
Chi-kvadrat (χ²)-test
Denne test antager nulhypotesen om, at alle studierne er homogene, eller at hvert studie måler en identisk effekt, og giver os en p-værdi til at teste denne hypotese. Hvis testens p-værdi er lav, kan vi forkaste hypotesen, og der er heterogenitet.
Da testen ofte ikke er følsom nok, og den forkerte udelukkelse af heterogenitet sker hurtigt, bruger mange forskere en p-værdi på < 0,1 i stedet for < 0,05 som grænseværdi.
I²
Denne test blev udviklet af professor Julian Higgins og har en teori om at måle omfanget af heterogenitet i stedet for at angive, om den er til stede eller ej.
Tærskler for fortolkningen af I² kan være misvisende, da betydningen af inkonsistens afhænger af flere faktorer. En grov vejledning til fortolkning er som følger:
For at forstå ovenstående teori skal man se på følgende eksempel.
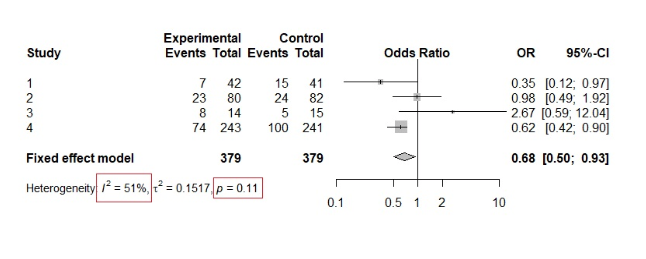
Vi kan se, at p-værdien af chi-kvadrat-testen er 0,11, hvilket bekræfter nulhypotesen og dermed tyder på homogenitet. Ved at se på interventionerne kan vi dog allerede nu se en vis heterogenitet i resultaterne. Desuden er I²-værdien 51 %, hvilket tyder på moderat til betydelig heterogenitet.
Dette er et godt eksempel på, hvordan χ²-testen kan være misvisende, når der kun er få undersøgelser i metaanalysen.
Hvordan håndterer man heterogenitet?
Når du har opdaget variabilitet i dine resultater, skal du håndtere den. Her er nogle trin til, hvordan du kan behandle dette problem:
- Kontroller dine data for fejl – Gå tilbage og se, om du måske har indtastet noget forkert
- Lad være med at lave en metaanalyse, hvis heterogeniteten er for høj – Ikke alle systematiske oversigter har brug for en metaanalyse
- Udforsk heterogeniteten – Dette kan gøres ved hjælp af subgruppeanalyse eller metaanalyse
- .regression
- Udfør en metaanalyse med tilfældige effekter – Husk, at denne fremgangsmåde er for heterogenitet, der ikke kan forklares, fordi den skyldes tilfældigheder
- Ændring af effektmålene – Lad os sige, at du bruger risikodifferencen og har høj heterogenitet, så prøv Risikoratio eller Odds Ratio
(1) Fletcher, J. Hvad er heterogenitet, og er det vigtigt? BMJ 2007; 334 :94
(3) https://www.mathsisfun.com/data/chi-square-test.html
