For et par år siden skrev Scott Fortmann-Roe et godt essay med titlen “Understanding the Bias-Variance Tradeoff.”
Da datavidenskab bliver til et anerkendt erhverv med sit eget sæt værktøjer, procedurer, arbejdsgange osv, synes der ofte at være mindre fokus på statistiske processer til fordel for de mere spændende aspekter (se her og her for et par eksempler på diskussioner).
Begrebsdefinitioner
Mens dette vil tjene som et overblik over Scotts essay, som du kan læse for yderligere detaljer og matematiske indsigter, vil vi starte med Fortmann-Roe’s ordrette definitioner, som er centrale for stykket:
Fejl på grund af bias: Fejl på grund af bias tages som forskellen mellem den forventede (eller gennemsnitlige) forudsigelse af vores model og den korrekte værdi, som vi forsøger at forudsige. Selvfølgelig har man kun én model, så det kan virke lidt mærkeligt at tale om forventede eller gennemsnitlige forudsigelsesværdier. Forestil dig imidlertid, at du kunne gentage hele modelopbygningsprocessen mere end én gang: hver gang du indsamler nye data og udfører en ny analyse og skaber en ny model. På grund af tilfældigheden i de underliggende datasæt vil de resulterende modeller have en række forudsigelser. Bias måler, hvor langt disse modellernes forudsigelser generelt er fra den korrekte værdi.
Fejl på grund af varians: Fejlen som følge af varians er variabiliteten af en modelforudsigelse for et givet datapunkt. Igen, forestil dig, at du kan gentage hele modelopbygningsprocessen flere gange. Variansen er, hvor meget forudsigelserne for et givet punkt varierer mellem forskellige realiseringer af modellen.
Væsentligt er bias, hvor langt væk en models forudsigelser er fra korrekthed, mens variansen er den grad, i hvilken disse forudsigelser varierer mellem modeliterationer.
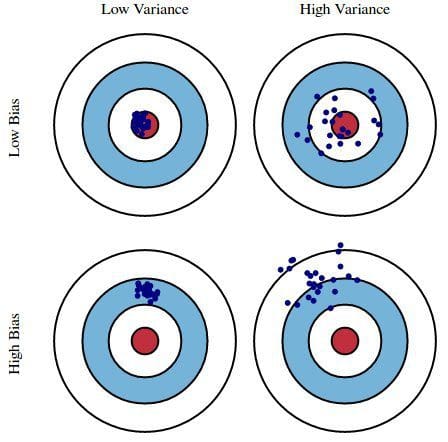
Fig. 1: Grafisk illustration af bias og varians
Fra Understanding the Bias-Variance Tradeoff, af Scott Fortmann-Roe.
Diskussion
Med en simpel fejlbehæftet præsidentvalgsundersøgelse som eksempel forklares fejlene i undersøgelsen derefter gennem de to briller af bias og varians: udvælgelse af undersøgelsesdeltagere fra en telefonbog er en kilde til bias; en lille stikprøvestørrelse er en kilde til varians; minimering af den samlede modelfejl er afhængig af en afbalancering af bias- og variansfejl.
Fortmann-Roe fortsætter derefter med at diskutere disse spørgsmål i forbindelse med en enkelt algoritme: k-Nærmeste Naboer. Han giver derefter nogle centrale spørgsmål at tænke over, når man håndterer bias og varians, herunder re-sampling-teknikker, asymptotiske egenskaber ved algoritmer og deres virkning på bias- og variansfejl og bekæmpelse af ens antagelser over for både data og deres modellering.
Afsnittet slutter med at hævde, at disse 2 begreber i deres kerne er tæt forbundet med både over- og undertilpasning. Efter min mening er her det vigtigste punkt:
Da der tilføjes flere og flere parametre til en model, stiger modellens kompleksitet, og variansen bliver vores primære bekymring, mens bias falder støt og roligt. For eksempel vil kompleksiteten af den resulterende model blive større, jo flere polynomiale termer der tilføjes til en lineær regression, jo større bliver den resulterende models kompleksitet. Med andre ord har bias en negativ førsteordensafledning som reaktion på modellens kompleksitet, mens varians har en positiv hældning.

Fig. 2: Bias og varians bidrager til den samlede fejl
Fra Understanding the Bias-Variance Tradeoff, af Scott Fortmann-Roe.
Fortmann-Roe afslutter afsnittet om over- og underpasning ved at henvise til et andet af sine gode essays (Accurately Measuring Model Prediction Error) og går derefter videre til den yderst anbefalingsværdige anbefaling om, at “resamplingbaserede foranstaltninger såsom krydsvalidering bør foretrækkes frem for teoretiske foranstaltninger såsom Aikakes informationskriterier”.
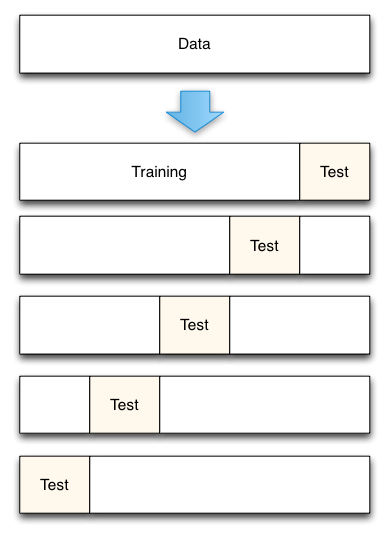
Fig. 3: 5-Fold cross-validation data split
Fra Accurately Measuring Model Prediction Error, af Scott Fortmann-Roe.
Naturligvis er antallet af foldninger, der skal anvendes ved krydsvalidering (k-fold krydsvalidering, ikke sandt?), værdien af k, en vigtig beslutning. Jo lavere værdien er, jo større bias i fejlskønnene og jo mindre varians. Omvendt, når k er sat lig med antallet af forekomster, er fejlskønnet så meget lavt i bias, men har mulighed for høj varians. Afvejningen mellem bias og varians er helt klart vigtig at forstå for selv de mest rutineprægede statistiske evalueringsmetoder som f.eks. k-fold krydsvalidering.
Desværre synes krydsvalidering også til tider at have mistet sin tiltrækningskraft i den moderne tidsalder inden for datalogi, men det er en diskussion til en anden gang.
Jeg anbefaler at læse hele Scott Fortmann-Roes essay om bias-varians tradeoff samt hans stykke om måling af modelprædiktionsfejl.
Relateret:
- Big Data, bibelkoder og Bonferroni
- Datavidenskab om variabel udvælgelse: En gennemgang
- Datasæt frem for algoritmer
