Link State Routing er en teknik, hvor hver router deler viden om sit nabolag med alle andre routere i internetnetværket.
De tre nøgler til at forstå Link State Routing-algoritmen:
- Viden om nabolaget: I stedet for at sende sin routingtabel sender en router kun oplysninger om sit nabolag. En router sender sine identiteter og omkostninger for de direkte tilknyttede forbindelser til andre routere.
- Flooding: Hver router sender oplysningerne til alle andre routere i internetværket undtagen til sine naboer. Denne proces er kendt som Flooding. Hver router, der modtager pakken, sender kopierne til alle sine naboer. Til sidst modtager hver enkelt router en kopi af de samme oplysninger.
- Informationsdeling: En router sender kun oplysningerne til alle andre routere, når der sker en ændring i oplysningerne.
Link State Routing har to faser:
Reliable Flooding
- Initialtilstand: Hver knude kender omkostningerne for sine naboer.
- Sluttilstand: Hver knude kender hele grafen.
Ruteberegning
Hver knude bruger Dijkstras algoritme på grafen til at beregne de optimale ruter til alle knuder.
- Link state routing-algoritmen er også kendt som Dijkstras algoritme, som bruges til at finde den korteste vej fra en knude til alle andre knuder i netværket.
- Dijkstras algoritme er en iterativ, og den har den egenskab, at efter den k-te iteration af algoritmen er de mindst omkostningsfulde stier velkendte for k destinationsknuder.
Lad os beskrive nogle notationer:
- c( i , j): Link cost fra node i til node j. Hvis i og j noder ikke er direkte forbundet, så er c(i , j) = ∞.
- D(v): Det definerer omkostningerne for den sti fra kildekode til destination v, der har de mindste omkostninger i øjeblikket.
- P(v): Den definerer den tidligere knude (nabo til v) sammen med den aktuelle vej med de mindste omkostninger fra kildekode til v.
- N: Det er det samlede antal knuder, der er tilgængelige i netværket.
Algoritme
InitializationN = {A} // A is a root node.for all nodes vif v adjacent to Athen D(v) = c(A,v)else D(v) = infinityloopfind w not in N such that D(w) is a minimum.Add w to NUpdate D(v) for all v adjacent to w and not in N:D(v) = min(D(v) , D(w) + c(w,v))Until all nodes in N
I ovenstående algoritme efterfølges et initialiseringstrin af løkken. Antallet af gange løkken udføres er lig med det samlede antal knuder, der er til rådighed i netværket.
Lad os forstå gennem et eksempel:
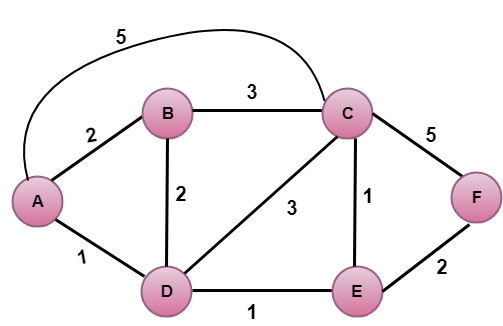
I ovenstående figur er kildevertexet A.
Strin 1:
Det første trin er et initialiseringstrin. Den i øjeblikket kendte mindste omkostningssti fra A til dens direkte tilknyttede naboer, B, C og D, er henholdsvis 2,5,1. Omkostningerne fra A til B er sat til 2, fra A til D er sat til 1 og fra A til C er sat til 5. Omkostningerne fra A til E og F er sat til uendelig, da de ikke er direkte forbundet med A.
| Stræk | N | D(B),P(B) | D(C),P(C) | D(D),P(D) | D(E),P(E) | D(F),P(F) | |
|---|---|---|---|---|---|---|---|
| 1 | A | 2,A | 5,A | 5,A | 1,A | ∞ | ∞ |
Stræk 2:
I ovenstående tabel kan vi konstatere, at toppunkt D indeholder den mindst omkostningsfulde vej i trin 1. Derfor er det tilføjet i N. Nu skal vi bestemme en mindst omkostningsfuld vej gennem toppunktet D.
a) Beregning af korteste vej fra A til B
b) Beregning af korteste vej fra A til C
c) Beregning af korteste vej fra A til E
Bemærk: Toppunktet D har ingen direkte forbindelse til toppunktet E. Derfor er værdien af D(F) uendelig.
| Step | N | D(B),P(B) | D(C),P(C) | D(D),P(D) | D(E),P(E) | D(F),P(F) | |
|---|---|---|---|---|---|---|---|
| 1 | A | 2,A | 5,A | 1,A | ∞ | ∞ | |
| 2 | AD | 2,A | 4,D | 2,D | ∞ |
Stræk 3:
I ovenstående tabel kan vi konstatere, at både E og B har den mindst omkostningstunge vej i trin 2. Lad os se på toppunktet E. Nu bestemmer vi den mindst omkostningsfulde vej for de resterende hjørner gennem E.
a) Beregning af den korteste vej fra A til B.
b) Beregning af den korteste vej fra A til C.
c) Beregning af den korteste vej fra A til F.
| Step | N | D(B),P(B) | D(C),P(C) | D(D),P(D) | D(E),P(E) | D(F),P(F) | ||
|---|---|---|---|---|---|---|---|---|
| 1 | A | 2,A | 5,A | 1,A | ∞ | ∞ | ∞ | |
| 2 | AD | 2,A | 4,D | 2,D | ∞ | |||
| 3 | ADE | 2,A | 3,E | 4,E |
Strin 4:
I ovenstående tabel kan vi se, at toppunkt B har den mindst omkostningsfulde vej i trin 3. Derfor tilføjes det i N. Nu bestemmer vi den mindst omkostningsfulde vej for de resterende toppunkter gennem B.
a) Beregning af den korteste vej fra A til C.
b) Beregning af den korteste vej fra A til F.
| Step | N | D(B),P(B) | D(C),P(C) | D(D),P(D) | D(E),P(E) | D(F),P(F) | ||
|---|---|---|---|---|---|---|---|---|
| 1 | A | 2,A | 5,A | 5,A | 1,A | ∞ | ∞ | |
| 2 | AD | 2,A | 4,D | 2,D | ∞ | |||
| 3 | ADE | 2,A | 3,E | 4,E | ||||
| 4 | ADEB | 3,E | 4,E |
Strin 5:
I ovenstående tabel kan vi konstatere, at C toppunktet har den mindst omkostningstunge sti i trin 4. Derfor er det tilføjet i N. Nu bestemmer vi den mindst omkostningsfulde vej for de resterende toppunkter gennem C.
a) Beregning af den korteste vej fra A til F.
| Step | N | D(B),P(B) | D(C),P(C) | D(D),P(D) | D(E),P(E) | D(F),P(F) | ||
|---|---|---|---|---|---|---|---|---|
| 1 | A | 2,A | 5,A | 1,A | ∞ | ∞ | ||
| 2 | AD | 2,A | 4,D | 2,D | ∞ | |||
| 3 | ADE | 2,A | 3,E | 4,E | ||||
| 4 | ADEB | 3,E | 4,E | |||||
| 5 | ADEBC | 4,E |
Den endelige tabel:
| Step | N | D(B),P(B) | D(C),P(C) | D(D),P(D) | D(E),P(E) | D(F),P(F) | ||||
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | A | 2,A | 5,A | 1,A | ∞ | ∞ | ||||
| 2 | AD | 2,A | 4,D | 2,D | ∞ | |||||
| 3 | ADE | 2,A | 3,E | 4,E | ||||||
| 4 | ADEB | ADEB | 3,E | 4,E | ||||||
| 5 | ADEBC | 4,E | ||||||||
| 6 | ADEBCF |
Ulempe:
Der skabes tung trafik i Line state-routing på grund af oversvømmelse. Flooding kan forårsage en uendelig looping, dette problem kan løses ved at bruge Time-to-leave-feltet
