En standardafvigelse er et tal, der fortæller os, i hvor høj grad et sæt tal ligger fra hinanden.En standardafvigelse kan være fra 0 til uendeligt. En standardafvigelse på 0 betyder, at en liste af tal alle er lige store – de ligger slet ikke fra hinanden i nogen grad.
Standardafvigelse – Eksempel
Fem ansøgere tog en IQ-test som en del af en jobansøgning. Deres resultater på tre IQ-komponenter er vist nedenfor.
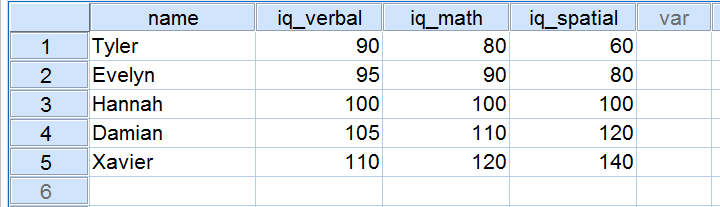
Nu skal vi se nærmere på resultaterne på de tre IQ-komponenter. Bemærk, at alle tre har et gennemsnit på 100 over vores 5 ansøgere. Scorerne på iq_verbal ligger dog tættere på hinanden end scorerne på iq_math. Desuden ligger scoren på iq_spatial længere fra hinanden end scoren på de to første komponenter. Det præcise omfang, hvori et antal scorer ligger fra hinanden, kan udtrykkes som et tal. Dette tal er kendt som standardafvigelsen.
Standardafvigelse – Resultater
I det virkelige liv inspicerer vi naturligvis ikke visuelt de rå resultater for at se, hvor langt de ligger fra hinanden. I stedet får vi simpelthen noget software til at beregne dem for os (mere om det senere). Tabellen nedenfor viser standardafvigelserne og nogle andre statistikker for vores IQ-data. Bemærk, at standardafvigelserne bekræfter det mønster, vi så i de rå data.
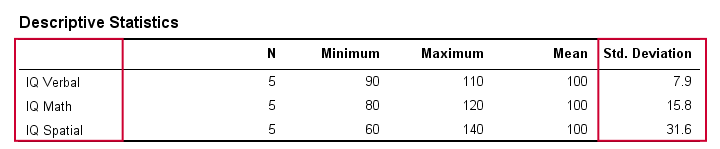
Standardafvigelse og histogram
Ret, lad os gøre tingene lidt mere visuelle. Figuren nedenfor viser standardafvigelserne og histogrammerne for vores IQ-scoringer. Bemærk, at hver søjle repræsenterer scoren for 1 ansøger på 1 IQ-komponent. Igen ser vi, at standardafvigelserne angiver, i hvor høj grad scorerne ligger fra hinanden.
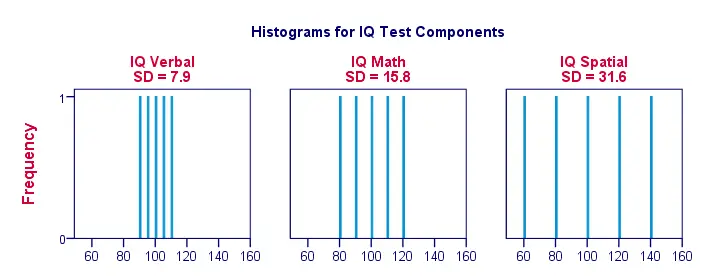
Standardafvigelse – flere histogrammer
Når vi visualiserer data på blot en håndfuld observationer som i den foregående figur, kan vi nemt se et klart billede. For at få et mere realistisk eksempel vil vi nedenfor præsentere histogrammer for 1.000 observationer. Det er vigtigt, at disse histogrammer har identiske skalaer; for hvert histogram svarer en centimeter på x-aksen til ca. 40 “IQ-komponentpunkter”.
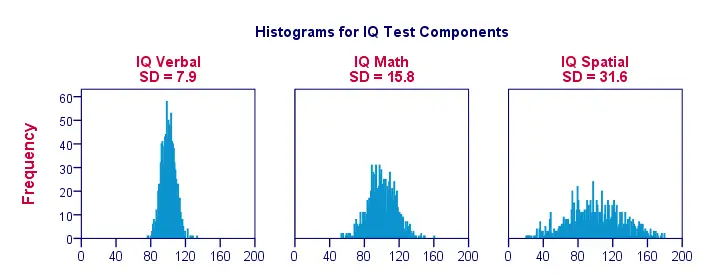
Bemærk, hvordan histogrammerne giver mulighed for grove skøn over standardafvigelser. ‘Bredere’ histogrammer indikerer større standardafvigelser; pointene (x-aksen) ligger længere fra hinanden. Da alle histogrammer har samme overflade (svarende til 1.000 observationer), er større standardafvigelser også forbundet med ‘bredere’ histogrammer.
Standardafvigelse – populationsformel
Så hvordan beregner din software standardafvigelser? Tja, den grundlæggende formel er
$$$\sigma = \sqrt{\frac{\sum(X – \mu)^2}{N}}}$$$$
hvor
- \(X\) betegner hvert enkelt tal;
- \(\mu\) betegner middelværdien over alle tal, og
- \(\sum\) betegner en sum.
Med andre ord er standardafvigelsen kvadratroden af den gennemsnitlige kvadrerede forskel mellem hvert enkelt tal og gennemsnittet af disse tal.
Vigtigt nok forudsætter denne formel, at dine data indeholder hele den pågældende population (deraf “populationsformel”). Hvis dine data kun indeholder et udsnit af din målpopulation, skal du se nedenfor.
Populationsformel – Software
Du kan bruge denne formel i Google ark, OpenOffice og Excel ved at skrive =STDEVP(...) i en celle. Angiv de tal, som du vil have standardafvigelsen over, mellem parenteserne, og tryk på Enter. Figuren nedenfor illustrerer ideen.
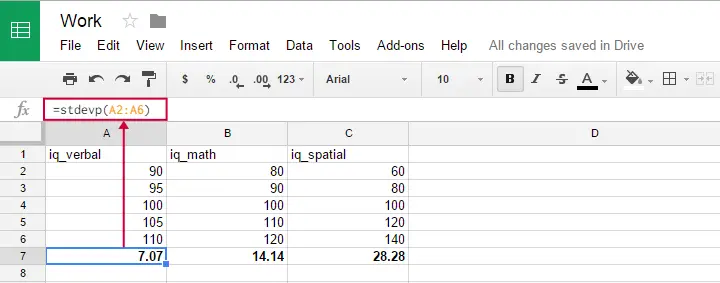
Der er mærkeligt nok, at formlen for populationens standardafvigelse tilsyneladende ikke findes i SPSS.
Standardafvigelse – stikprøveformel
Nu kommer vi til noget udfordrende: Hvis dine data er (omtrent) en simpel tilfældig stikprøve fra en eller anden (meget) større population, vil den foregående formel systematisk undervurdere standardafvigelsen i denne population. En ubiased estimator for populationens standardafvigelse fås ved at bruge
$$$$S_x = \sqrt{\frac{\sum(X – \overline{X})^2}{N -1}}}$$$
Med hensyn til beregningerne er den store forskel i forhold til den første formel, at vi dividerer med \(n -1\) i stedet for \(n\). Dividerer man med et mindre tal, får man et (lidt) større resultat. Dette kompenserer netop for den førnævnte undervurdering. For store stikprøvestørrelser har de to formler dog stort set identiske resultater.
I GoogleSheets, Open Office og MS Excel bruger STDEV-funktionen denne anden formel. Det er også den (eneste) standardafvigelsesformel, der er implementeret i SPSS.
Standardafvigelse og varians
Et andet tal, der udtrykker, hvor langt et sæt tal ligger fra hinanden, er variansen. Variansen er den kvadrerede standardafvigelse. Dette indebærer, at variansen i lighed med standardafvigelsen har en populationsformel såvel som en stikprøveformel.
I princippet er det ubehageligt, at to forskellige statistikker grundlæggende udtrykker den samme egenskab ved et sæt tal. Hvorfor kasserer vi ikke bare variansen til fordel for standardafvigelsen (eller omvendt)? Det grundlæggende svar er, at standardafvigelsen har mere ønskværdige egenskaber i nogle situationer og variansen i andre.
