Beregning af tid, indsats og omkostninger er en af de mest kritiske dele af projektledelse. Dette skyldes den grundlæggende betydning af disse skøn for hele projektplanlægningen og især for omfanget, tidsplanen og omkostningsbaseline. En af de estimeringsteknikker, der foreslås i PMI’s Project Management Body of Knowledge (PMBOK 6th ed., kap. 6.4, 7.2), er trepunktsskønnet, der anvendes med trepunktsfordelingen, beta- eller PERT-fordelingen. Vi vil introducere disse metoder i denne artikel.
Hvad er trepunktsskønsteknikken?
Det trepunktsskøn er en enkel, men nyttig metode til at skønne tid eller omkostninger for arbejdsemner. I henhold til PMI-metodologien anvendes den i procesgrupperne “Estimate Activity Duration” og “Estimate Costs”. Teknikken omfatter tre forskellige estimater, der normalt indhentes fra fageksperter:
- Optimistisk estimat,
- Pessimistisk estimat,
- Mest sandsynligt estimat.
Det optimistiske estimat er den forventede mængde arbejde eller tid, der er nødvendig for at udføre en aktivitet, hvis man antager, at der ikke opstår hindringer, og at alt forløber glat. Det repræsenterer det såkaldte best-case-scenarie. Det pessimistiske punkt er baseret på den antagelse, at det modsatte var tilfældet – det repræsenterer det værst tænkelige scenarie. Selv om begge estimater henviser til yderpunkterne i intervallet af forventede resultater, formodes estimaterne at være nogenlunde realistiske.
Det tredje punkt afspejler det mest sandsynlige tilfælde, det er det estimat af arbejde eller tid, der anses for at være det mest realistiske. Man kunne være fristet til blot at bruge gennemsnittet mellem det optimistiske og det pessimistiske punkt uden at tænke nærmere over det. Dette er dog ikke nødvendigvis hensigtsmæssigt i mange tilfælde. I praksis er det normalt værd at bestemme dette mest sandsynlige skøn korrekt, analogt med de andre skønspunkter.
Resultatet af trepunktsskønnet er en såkaldt trekantet fordeling af tidsværdier eller omkostningsbeløb, der består af de tre skøn (se illustrationen nedenfor).
Hvad er PERT?
PERT står for Program Evaluation and Review Technique og blev udviklet som et avanceret system til planlægning og styring af projekttidsplaner af den amerikanske flåde i 1950’erne (kilde: Heldman, PMP Study guide, kap. 4).
En anden, ikke alt for seriøs, historie om dets oprindelse blev engang offentliggjort af en anonym forfatter i PMI’s tidsskrift (Link; kilde: Anonym (1975). PERT-the hoax of the century. Project Management Quarterly, 6(3), 22-23).
I projekter i PMI-stil anvendes PERT primært som en supplerende teknik til den kritiske vejmetode til planlægning af aktiviteter. Den kan dog også anvendes til selvstændige estimater af arbejdsemner og aktiviteter.
Den såkaldte PERT-fordeling udnytter de værdier, der er fastlagt ved hjælp af trepunktsmetoden. Den kan i princippet anvendes til alle planlægningsniveauer, lige fra aktiviteter til hele projekter. Det kan dog kræve en vis kritisk og konceptuel tænkning at finde den rette granularitet til meningsfuld estimering.
PERT-metoden indebærer en overvægtning af det “mest sandsynlige” estimat. Den omdanner trepunktsskønnet til en klokkeformet kurve og gør det muligt at bestemme sandsynlighederne for intervaller af forventede værdier.
Hvad er forskellene mellem trepunktsskøn og PERT-fordelingen af trepunktsskøn?
Mens den trekantede fordeling kun tager hensyn til de tre skønnede punkter, gør PERT-metoden det muligt at omdanne trepunktsskønnet til en klokkeformet, næsten normalfordelt kurve og kan således anvendes til beregning af sandsynlighederne for intervaller af forventede værdier.
Det følgende diagram illustrerer forskellene mellem PERT-fordelingen, den trekantede fordeling og en fremstilling af trepunktsskønnet, som om det var en normalfordeling.
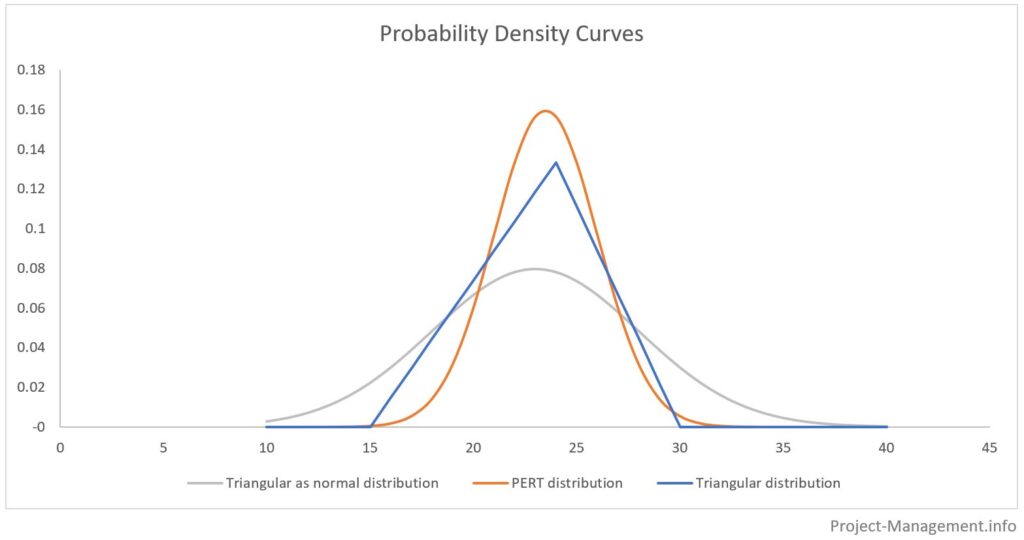
Arealerne under sandsynlighedsfordelingskurverne repræsenterer de kumulative sandsynligheder for de respektive intervaller af skøn. Typisk bestemmes disse intervaller med den forventede værdi +/- standardafvigelse multipliceret med 1, 2 og 3. Dette er illustreret i følgende figur:
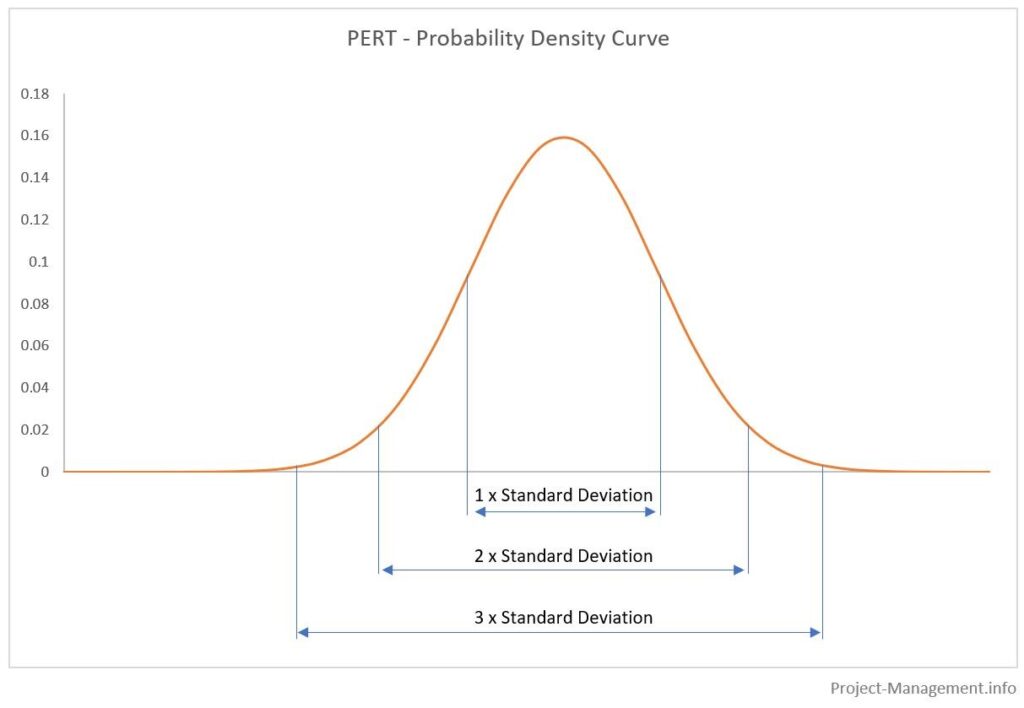
De resulterende sandsynligheder (ca.) er
- 68,3 % for 1 standardafvigelse,
- 95.5% for 2 standardafvigelser,
- 99,7% for 3 standardafvigelser.
Den viden, der kræves til PMP-eksamen, er begrænset til at beregne de forventede estimater og være bekendt med de forskellige sandsynligheder (kilde). Derfor vil vi ikke dække de statistiske detaljer og baggrunden i denne artikel – du kan finde disse detaljer på Riskamp.
Brug denne beregner til at bestemme trepunktsskøn og PERT.
Hvordan beregnes trepunktsskøn?
Den trekantede fordeling
Den enkle, men almindeligt anvendte beregning involverer gennemsnittet eller middelværdien af de 3 estimerede værdier. Formlen for denne trekantfordeling er:
E =(O + M + P) / 3
hvor:
E = Forventet tids- eller omkostningsbeløb,
O = Optimistisk skøn,
M = Mest sandsynligt skøn,
P = Pessimistisk skøn.
PMBOK anvender t(E), t(O), t(M) og t(P) som variabler for tidsestimater og c(E), c(O), c(M) og c(P).
Vægten af hvert estimat i denne ligning er identisk. Det “mest sandsynlige” tilfælde påvirker således ikke det endelige skøn mere end de to mindre sandsynlige skøn. Dette er forskelligt fra betadistributionsmetoden.
Den PERT-betafordeling
Den PERT-betafordeling tager hensyn til, at det “mest sandsynlige” tilfælde er mere sandsynligt, hvilket afspejles i en multiplikator for dette estimat. PMI-metoden foreslår denne beregning som et alternativ til den trekantede fordeling for omkostningsestimater (vi er dog af den opfattelse, at den også kan anvendes til tidsestimater).
I denne metode får det mest sandsynlige estimat en multiplikator på 4, mens den samlede divisor øges til 6. Formlen er som følger:
E =(O + 4*M + P) / 6
hvor:
E = Forventet tids- eller omkostningsbeløb,
O = Optimistisk skøn,
M = Mest sandsynligt skøn,
P = Pessimistisk skøn.
Standardafvigelsen for PERT-fordelingen beregnes ved hjælp af formlen:
Standardafvigelse = (P – O) / 6
Til estimering af en hel vej (analog kritisk vejmetode) anvendes et lignende koncept, dog ved hjælp af en kombineret standardafvigelse for alle aktiviteter.
Eksempel på et trepunktsskøn og PERT
Et team af fageksperter vurderer den tid, det tager at gennemføre en aktivitet. I dette eksempel estimeres en aktivitets varighed ved hjælp af trepunkts estimeringsteknikken.De kommer frem til følgende tal:
| Optimistisk skøn | 15 dage |
| Pessimistisk skøn | 24 dage |
| Mest sandsynligt skøn | 30 dage |
Værdierne spænder fra 15 dage (optimistisk)til 30 dage (pessimistisk). En varighed på 24 dage anses for at være den mest sandsynligetid, der er nødvendig for at afslutte arbejdet.
Beregning af den forventede varighed med en trekantfordeling
Den forventede varighed ved hjælp af en trekantfordeling beregnes som følger:
Slutskøn = (15 + 30 + 24) / 3.
Det resulterende endelige skøn efter denne metode er 23, hvilket grundlæggende er det uvægtede gennemsnit af de tre skøn.
Beregning af den forventede varighed ved hjælp af PERT Beta-fordeling
Den forventede varighed kan også beregnes med PERT-metoden:
Slutskøn (forventet værdi) = (15 + 4×24 + 30) / 6.
Den resulterende forventede værdi er 23,5 dage, hvilket er større end det endelige skøn, der er fastsat efter den trekantede metode. Dette skyldes den højere vægt (dvs. multiplikator på 4), der tildeles det “mest sandsynlige” skøn.
Standardafvigelsen for dette skøn er:
Standardafvigelse = (30 – 15) / 6 = 2,5
Bestemmelse af sandsynlighederne for den forventede varighed
Når projektlederen har beregnet den forventede varighed og standardafvigelsen, kan han bestemme sandsynlighederne (ca.):
| Interval | Sandsynlighed | Nedre grænse | Øvre grænse | |
| 1 x standardafvigelse | 68.3% | 21 | 26 | |
| 2 x standardafvigelse | 95.5% | 18,5 | 28,5 | |
| 3 x standardafvigelse | 99.7% | 31 |
Med 68,3% sandsynlighed vil varigheden af aktiviteten være mellem 21 og 26 dage. For et interval på 18,5 til 28,5 dage er sandsynligheden 95,5 %. Anvendelse af 3 standardafvigelser dækker næsten alle datapunkter og bestemmer en sandsynlighed på 99,7 % for, at varigheden i sidste ende vil ligge mellem 16 og 31 dage.
Summary
Det endelige skøn efter trekantsmetoden var 23, sammenlignet med 23,5 efter PERT-metoden. Dette skyldes, at sidstnævnte tildeler en højere vægt til det “mest sandsynlige” tilfælde, som i vores tilfælde ikke nøjagtigt er gennemsnittet (eller det uvægtede gennemsnit af det optimistiske og det pessimistiske skøn.
Ved anvendelse af PERT-metoden kan der tages hensyn til sandsynlighederne for værdiintervaller. Dette er nyttigt, hvis kvaliteten af estimater varierer, f.eks. hvis forskellen mellem optimistiske og pessimistiske estimater afviger betydeligt mellem forskellige aktiviteter. I dette tilfælde vil brugen af intervaller og deres sandsynligheder afspejle spredningen og tillidsniveauet for de underliggende estimater.
Slutning
Skatningen af aktiviteter med hensyn til deres tids- og omkostningskrav er afgørende for planlægningen og skemalægningen af projekter og aktiviteter. I mange projekter findes der ikke mere nøjagtige estimater, f.eks. parametriske estimater baseret på statistiske korrelationer af f.eks. sammenlignelige projekter i fortiden. Trepunktsskønsmetoden er en god metode til at behandle og afbalancere top-down- eller fagekspertskøn i sådanne situationer.
PERT-fordelingen er sandsynligvis den mest nøjagtige metode til at samle disse værste, bedste og mest sandsynlige tilfælde i et enkelt tal (forventet værdi) eller et interval af værdier. Takket være brugen af standardafvigelsen tager den hensyn til både de iboende usikkerheder og den potentielle spredning af skøn.
Det er måske grunden til, at PERT stadig er en almindelig metode inden for projektoverslag og -planlægning, selv om den har eksisteret i nogle årtier og allerede kunne være blevet brugt af vores bedsteforældre (hvis de havde været projektledere).
