Buckinghamin Pi-teoremin soveltaminen

Seuraava: Edellinen: Buckinghamin pii-teoreema

Buckinghamin pii-teoremin soveltaminen

Asittamamme teoreema on hyvin yleinen, mutta se ei suinkaan rajoitu vain nestemekaniikkaan. Sitä käytetään monilla eri aloilla, kuten kasvitieteissä ja yhteiskuntatieteissä, ja aiheesta on kirjoitettu kirjoja ja niteitä. Emme kuitenkaan tarvitse paljon teoriaa voidaksemme soveltaa sitä. Tarkastelemme menettelytapaa, jolla teoreemaa voidaan käyttää ja jonka avulla saadaan tietylle virtaukselle ei-ulotteiset luvut.

1. Luettele kaikki prosessia säätelevät muuttujat.
   1. Luettele kaikki prosessia säätelevät muuttujat. Näiden muuttujien tulisi olla toisistaan riippumattomia. Esimerkiksi ei pitäisi valita tiheyttä, painovoimaa ja ominaispainoa. Tiheyden ja ominaispainon pitäisi riittää. Ongelmaamme varten meillä on F, D, V, ja . Meillä on n = 5.
   2. Merkitse toistuvat muuttujat. Meidän tapauksessamme nämä ovat D, V ja , jolloin k = 3 .
   3. Päättele, kuinka monta ei-ulotteista lukua on. Meidän tapauksessamme on n – k = 2. Ongelmassamme on 2 ei-ulotteista lukua, ja .
   4. Määrittele ei-ulotteiset luvut ryhmittelemällä muuttujat n – k ryhmiin siten, että jokaisessa ryhmässä on kaikki toistuvat muuttujat ja yksi ei-toistuva muuttuja. Näin ollen ongelmassamme on

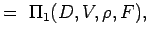
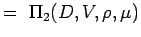
      		(5.2)
      Let
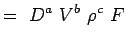
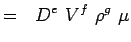
      		(5.3)

   5. Muodostetaan nyt kukin muuttuja dimensioina. Käytetään MLT-järjestelmää, jonka mukaan ongelmiemme muuttujilla on seuraavat ulottuvuudet.
      

      Muuttuja	Dimensiot
      F, Voima	M L / T2 tai M L T-2
      D, Halkaisija:	L
      V, Nopeus	L/T tai LT-1
      , Tiheys:	M/L3 tai ML-3
      , Viskositeetti	ML-1T-1

      Substituoimalla nämä mitat yhtälöön. 5.2, saadaan

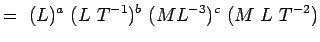
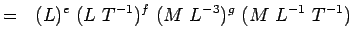
      		(5.4)
      Or
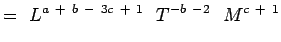
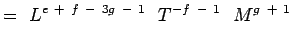
      		(5.5)

      Huomauttamalla, että ja ovat dimensiottomia, saadaan,

      a + b – 3c + 1 = 0; -b – 2 = 0, c + 1 = 0
      e + f – 3g – 1 = 0; -f – 1 = 0;g + 1 = 0	(5.6)

      Yhtälöitä ratkaisemalla saadaan,

      a = -2, b = -2, c = -1
      e = -1, f = -1, g = -1	(5.7)

      Jatkossa ei-ulotteisista luvuistamme tulee,

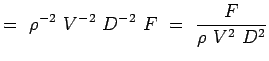
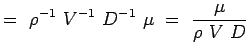
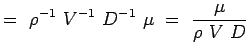
      				(5.8)

   Siten olemme löytäneet ei-ulotteiset luvut kiinnostavalle virtaukselle, nimittäin vetovastukselle pyöreän sylinterin ympäri. Näiden kahden luvun välinen funktionaalinen suhde voidaan ilmaista seuraavasti:

   Huomaa kuitenkin, että johtamamme termin 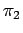muoto on hieman erilainen kuin alussa oletimme. Yhtälön oikea puoli on itse asiassa Reynoldsin luvun käänteisluku!Tämä osoittaa analyysin haittapuolen, jonka mukaan lukujen 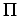välistä tarkkaa funktionaalista muotoa ei voida saada. Mitään saatua kerrointa tai indeksiä ei voida määrittää tällä analyysillä. Ne olisi määritettävä kokeellisesti tai laskennallisesti. Mutta koska luvut ovat dimensiottomia, voimme kirjoittaa,

   
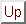
   Jatkossa: Edellinen: Buckinghamin piteoreema

   (c) Aerospace, Mechanical & Mechatronic Engg. 2005
   Sydneyn yliopisto