Posted on 29th November 2018 by Maximilian Siebert
Heterogeenisuutta ei kannata pelätä, se tarkoittaa vain sitä, että datassasi on vaihtelua. Jos siis kootaan yhteen eri tutkimuksia niiden analysointia tai meta-analyysin tekemistä varten, on selvää, että eroja löytyy. Heterogeenisuuden vastakohta on homogeenisuus, joka tarkoittaa, että kaikki tutkimukset osoittavat saman vaikutuksen.
On tärkeää huomata, että heterogeenisuutta on erityyppisiä:
- Kliininen: Erot osallistujissa, interventioissa tai tuloksissa
- Metodologinen: Erot tutkimusasetelmassa, harhan riski
- Tilastollinen: Vaihtelu intervention vaikutuksissa tai tuloksissa
Olemme kiinnostuneita näistä eroista, koska ne voivat viitata siihen, että interventiomme ei ehkä toimi samalla tavalla joka kerta, kun sitä käytetään. Tutkimalla näitä eroja voidaan päästä paljon parempaan ymmärrykseen siitä, mitkä tekijät vaikuttavat interventioon ja millaista tulosta voidaan odottaa seuraavalla kerralla, kun interventio otetaan käyttöön.
Vaikka kliininen ja metodologinen heterogeenisuus ovat tärkeitä, tässä blogissa keskitytään tilastolliseen heterogeenisuuteen.
Miten heterogeenisuutta tunnistetaan ja mitataan
Silmälasitesti
Katso metsäkuvioissasi päällekkäisiä luottamusvälejä sen sijaan, että katsoisit, kummalla puolella vaikutusestimaattisi ovat. Se, ovatko tulokset vaikutuksettomuusviivan kummallakin puolella, ei välttämättä vaikuta arviointiisi siitä, onko heterogeenisuutta, mutta se voi vaikuttaa arviointiisi siitä, onko heterogeenisyydellä merkitystä.
Tämä mielessäsi katso alla olevaa kuvaajaa ja päätä, kumpi kuvaaja on homogeenisempi.
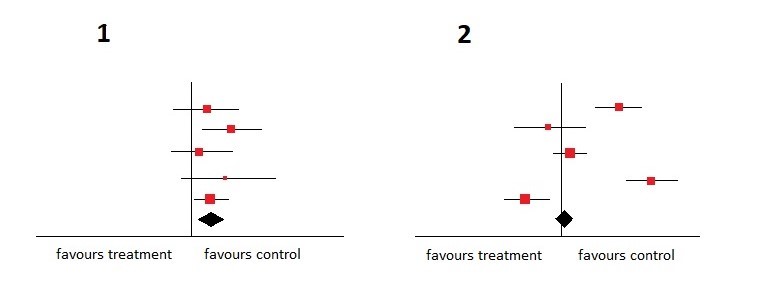
Homogeenisempi on tietysti kuvaaja numero 1 . Luottamusvälit ovat kaikki päällekkäisiä, ja lisäksi kaikki tutkimukset suosivat kontrolliinterventiota.
Neille, jotka rakastavat asioiden mittaamista pelkän silmäilyn sijaan, ei hätää, on vielä olemassa joitakin tilastollisia menetelmiä, jotka auttavat sinua tarttumaan heterogeenisuuden käsitteeseen.
Chi-neliö (χ²)-testi
Tässä testissä oletetaan nollahypoteesi, että kaikki tutkimukset ovat homogeenisia eli että jokainen tutkimus mittaa identtistä vaikutusta, ja annetaan p-arvo tämän hypoteesin testaamiseksi. Jos testin p-arvo on pieni, voimme hylätä hypoteesin ja heterogeenisuus on olemassa.
Koska testi ei usein ole riittävän herkkä ja heterogeenisuuden väärä poissulkeminen tapahtuu nopeasti, monet tutkijat käyttävät raja-arvona p-arvoa < 0,1 eikä < 0,05.
I²
Tämän testin kehitti professori Julian Higgins, ja sen teoria mittaa heterogeenisuuden laajuutta sen sijaan, että se toteaisi, onko heterogeenisuutta vai ei.
I²:n tulkintakynnykset voivat olla harhaanjohtavia, sillä epäjohdonmukaisuuden merkitys riippuu useista tekijöistä. Karkea tulkintaohje on seuraava:
Yllä olevan teorian ymmärtämiseksi tarkastellaan seuraavaa esimerkkiä.
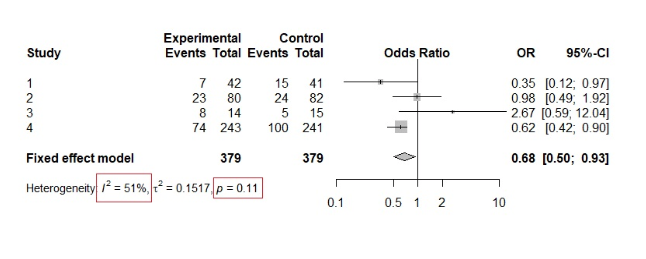
Voidaan nähdä, että khiin neliö -testin p-arvo on 0,11, mikä vahvistaa nollahypoteesin ja viittaa siten homogeenisuuteen. Tarkastelemalla interventioita voimme kuitenkin nähdä jo jonkin verran heterogeenisuutta tuloksissa. Lisäksi I²-arvo on 51 %, mikä viittaa kohtalaiseen tai huomattavaan heterogeenisuuteen.
Tämä on hyvä esimerkki siitä, miten χ²-testi voi olla harhaanjohtava, kun meta-analyysissä on vain muutama tutkimus.
Miten käsitellä heterogeenisuutta?
Kun olet havainnut vaihtelua tuloksissasi, sinun täytyy käsitellä sitä. Seuraavassa on muutamia vaiheita siitä, miten voit käsitellä tätä asiaa:
- Tarkista aineistosi virheiden varalta – Palaa takaisin ja katso, oletko kenties kirjoittanut jotain väärin
- Älä tee meta-analyysiä, jos heterogeenisuus on liian suurta – Kaikki systemaattiset katsaukset eivät tarvitse meta-analyysiä
- Tutki heterogeenisuutta – Tämä voidaan tehdä alaryhmäanalyysillä tai meta-regressiolla
- Toteuta satunnaisvaikutusten meta-analyysi – Muista, että tämä lähestymistapa on tarkoitettu heterogeenisuuteen, jota ei voida selittää, koska se johtuu sattumasta
- Muuttamalla vaikutusmittoja – Oletetaan, että käytät riskieroa ja heterogeenisuus on suuri, kokeile sitten Risk Ratio tai Odds Ratio
(1) Fletcher, J. Mitä heterogeenisuus on ja onko se tärkeää? BMJ 2007; 334 :94
(3) https://www.mathsisfun.com/data/chi-square-test.html
