Muutama vuosi sitten Scott Fortmann-Roe kirjoitti loistavan esseen otsikolla ”Understanding the Bias-Variance Tradeoff.”
Kun datatieteet muuttuvat hyväksytyksi ammattikunnaksi, jolla on omat työkalunsa, menettelytapansa, työnkulkunsa jne, näyttää usein siltä, että tilastollisiin prosesseihin kiinnitetään vähemmän huomiota jännittävämpien näkökohtien hyväksi (ks. pari esimerkkikeskustelua täältä ja täältä).
Käsitteellisiä määritelmiä
Kun tämä toimii yleiskatsauksena Scottin esseeseen, jonka voit lukea tarkempien yksityiskohtien ja matemaattisten oivallusten saamiseksi, aloitamme Fortmann-Roen sanatarkoilla määritelmillä, jotka ovat teoksen kannalta keskeisiä:
Error due to Bias: Virheeksi, joka johtuu vinoutumasta, katsotaan mallimme odotetun (tai keskimääräisen) ennusteen ja oikean arvon, jota yritämme ennustaa, välinen ero. Sinulla on tietysti vain yksi malli, joten odotetuista tai keskimääräisistä ennustearvoista puhuminen saattaa tuntua hieman oudolta. Kuvittele kuitenkin, että voisit toistaa koko mallinrakennusprosessin useammin kuin kerran: joka kerta kun keräät uusia tietoja ja suoritat uuden analyysin, luot uuden mallin. Koska taustalla olevissa tietokokonaisuuksissa on satunnaisuutta, tuloksena syntyvillä malleilla on ennusteiden vaihteluväli. Harha mittaa, kuinka kaukana näiden mallien ennusteet yleisesti ottaen ovat oikeasta arvosta.
Variaatiosta johtuva virhe: Varianssista johtuvaa virhettä pidetään mallin ennusteen vaihteluna tietylle datapisteelle. Kuvitellaan taas, että koko mallin rakennusprosessi voidaan toistaa useita kertoja. Varianssi on se, kuinka paljon ennustukset tietylle pisteelle vaihtelevat mallin eri realisointien välillä.
Välttävästi harha on se, kuinka kaukana mallin ennusteet ovat oikeellisuudesta, kun taas varianssi on se, kuinka paljon nämä ennusteet vaihtelevat mallin iteraatioiden välillä.
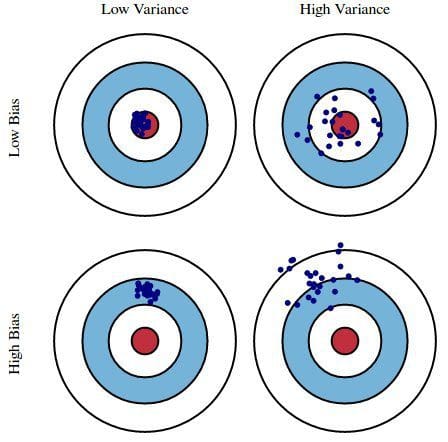
Kuva 1: Graafinen havainnollistus harhasta ja varianssista
Lähteestä Understanding the Bias-Variance Tradeoff, Scott Fortmann-Roe.
Keskustelu
Käyttäen esimerkkinä yksinkertaista virheellistä presidentinvaalitutkimusta, tutkimuksessa esiintyviä virheitä selitetään sitten harhan ja varianssin kaksoislinssin kautta: tutkimukseen osallistujien valitseminen puhelinluettelosta on harhan lähde; pieni otoskoko on varianssin lähde; mallin kokonaisvirheen minimointi perustuu harhan ja varianssin virheiden tasapainottamiseen.
Fortmann-Roe jatkaa sitten keskustelua näistä kysymyksistä, kun ne liittyvät yhteen algoritmiin: k-Nearest Neighbor. Sen jälkeen hän esittelee joitakin keskeisiä asioita, joita kannattaa miettiä harhojen ja varianssin hallinnassa, mukaan lukien uudelleennäytteenottotekniikat, algoritmien asymptoottiset ominaisuudet ja niiden vaikutus harhojen ja varianssin virheisiin sekä omien olettamusten torjuminen sekä datan että sen mallintamisen suhteen.
Essays päättyy väittäen, että pohjimmiltaan nämä kaksi käsitettä ovat tiukasti sidoksissa sekä yli- että alikorjaukseen. Mielestäni tässä on tärkein kohta:
Kun malliin lisätään yhä enemmän parametreja, mallin monimutkaisuus kasvaa ja varianssista tulee ensisijainen huolenaiheemme, kun taas harha vähenee tasaisesti. Esimerkiksi mitä enemmän polynomitermejä lisätään lineaariseen regressioon, sitä suurempi on tuloksena olevan mallin monimutkaisuus. Toisin sanoen biasilla on negatiivinen ensimmäisen kertaluvun derivaatta vasteena mallin monimutkaisuuteen, kun taas varianssilla on positiivinen kaltevuus.

Kuvio 2: Biasin ja varianssin osuus kokonaisvirheestä
Kuvio 2: Biasin ja varianssin osuus kokonaisvirheestä
Lähteestä Understanding the Bias-Variance Tradeoff, kirjoittanut Scott Fortmann-Roe.
Fortmann-Roe päättää yli- ja alimitoitusta käsittelevän osion viittaamalla toiseen hienoon esseeseensä (Accurately Measuring Model Prediction Error) ja siirtyy sitten erittäin kannatettavaan suositukseen, jonka mukaan ”resampling-pohjaisia mittareita, kuten ristiinvalidointia, tulisi suosia teoreettisten mittareiden, kuten Aikaken informaatiokriteerien, sijasta”.
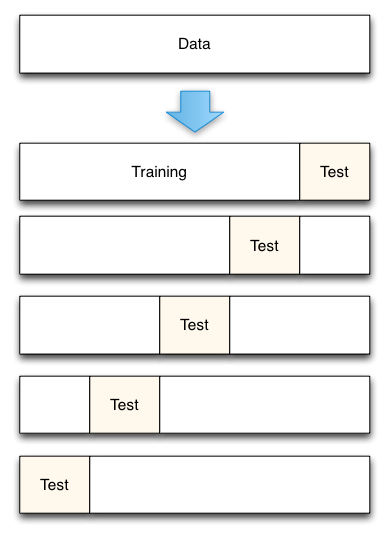
Kuva 3: 5-kertainen ristiinvalidointidatan jako
Kirjasta Accurately Measuring Model Prediction Error, Scott Fortmann-Roe.
Ristiinvalidoinnissa käytettävien kertausten määrä (k-kertainen ristiinvalidointi, eikö?), k:n arvo, on tietenkin tärkeä päätös. Mitä pienempi arvo, sitä suurempi harha virheestimaateissa ja sitä pienempi varianssi. Kääntäen, kun k asetetaan yhtä suureksi kuin instanssien lukumäärä, virhearvion harha on tällöin hyvin pieni, mutta siinä voi olla suuri varianssi. Harhan ja varianssin välinen kompromissi on selvästi tärkeä ymmärtää jopa kaikkein rutiininomaisimmissa tilastollisissa arviointimenetelmissä, kuten k-kertaisessa ristiinvalidoinnissa.
Valitettavasti ristiinvalidointi näyttää myös ajoittain menettäneen viehätyksensä nykyaikaisessa datatieteessä, mutta siitä keskustellaan toisen kerran.
Suosittelen lukemaan Scott Fortmann-Roen koko bias-variance tradeoff -esseen sekä hänen kirjoituksensa mallien ennustusvirheen mittaamisesta.
Related:
- Big Data, Bible Codes, and Bonferroni
- Data Science of Variable Selection: A Review
- Datasarjat yli algoritmien
