Keskihajonta on luku, joka kertoo, kuinka kaukana toisistaan joukko lukuja on toisistaan.Keskihajonta voi vaihdella 0:sta äärettömään. Keskihajonta 0 tarkoittaa, että joukko lukuja on yhtä suuri – ne eivät eroa toisistaan lainkaan.
Keskihajonta – Esimerkki
Viisi hakijaa teki älykkyystestin osana työhakemusta. Heidän pisteensä kolmesta ÄO-komponentista näkyvät alla.
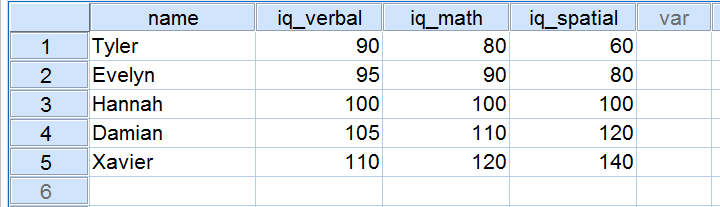
Katsotaan nyt tarkemmin kolmen ÄO-komponentin pistemääriä. Huomaa, että kaikkien kolmen keskiarvo on 100 viidellä hakijallamme. iq_verbal-pisteet ovat kuitenkin lähempänä toisiaan kuin iq_math-pisteet. Lisäksi iq_spatiaalisen osa-alueen pisteet ovat kauempana toisistaan kuin kahden ensimmäisen osa-alueen pisteet. Se, kuinka kaukana pisteet ovat toisistaan, voidaan ilmaista lukuna. Tätä lukua kutsutaan keskihajonnaksi.
Keskihajonta – Tulokset
Todellisessa elämässä emme luonnollisestikaan tarkastele raakapisteitä silmämääräisesti nähdaksemme, kuinka kaukana ne ovat toisistaan. Sen sijaan annamme jonkin ohjelmiston yksinkertaisesti laskea ne puolestamme (siitä lisää myöhemmin). Alla olevassa taulukossa esitetään älykkyysosamäärätietojen keskihajonnat ja joitakin muita tilastoja. Huomaa, että keskihajonnat vahvistavat raakadatassa havaitsemamme mallin.
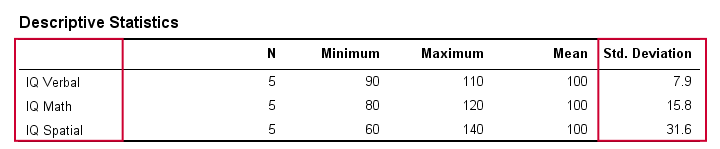
Keskihajonta ja histogrammi
Oikea, tehdään asioista hieman visuaalisempia. Alla olevassa kuvassa näkyvät IQ-pisteidemme keskihajonnat ja histogrammit. Huomaa, että kukin palkki edustaa yhden hakijan pistemäärää yhdessä ÄO-komponentissa. Jälleen kerran näemme, että keskihajonnat osoittavat, kuinka paljon pisteet ovat toisistaan erillään.
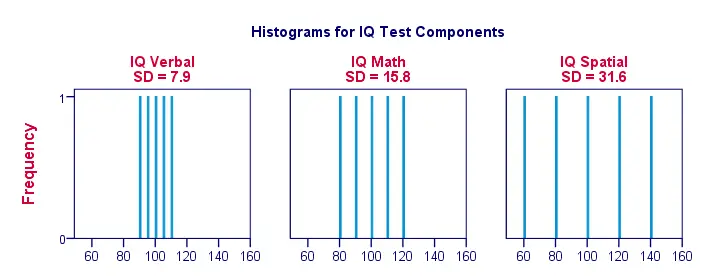
Keskihajonta – lisää histogrammeja
Kun visualisoimme tietoja vain muutamasta havainnosta kuten edellisessä kuviossa, näemme helposti selkeän kuvan. Realistisemman esimerkin vuoksi esitämme jäljempänä histogrammit 1000 havainnolle. On tärkeää, että näillä histogrammeilla on identtiset mittakaavat; jokaisessa histogrammissa yksi senttimetri x-akselilla vastaa noin 40:tä ”IQ-komponenttipistettä”.
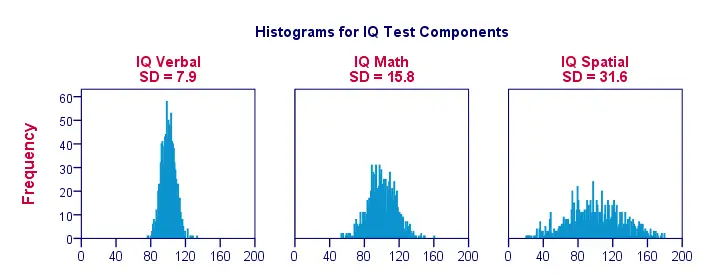
Huomaa, miten histogrammit mahdollistavat karkeat arviot keskihajonnoista. ”Leveämmät” histogrammit osoittavat suurempia keskihajontoja; pisteet (x-akseli) sijaitsevat kauempana toisistaan. Koska kaikilla histogrammeilla on identtiset pinta-alat (vastaavat 1000 havaintoa), suuremmat keskihajonnat liittyvät myös ”matalampiin” histogrammeihin.
Standardipoikkeama – Populaatiokaava
Miten ohjelmistosi laskee standardipoikkeamat? No, peruskaava on
$$\sigma = \sqrt{\frac{\sum(X – \mu)^2}{N}}$$
jossa
- \(X\) tarkoittaa jokaista erillistä lukua;
- \(\mu\) tarkoittaa kaikkien lukujen keskiarvoa ja
- \(\sum\) tarkoittaa summaa.
Sanalla sanoen keskihajonta on neliöjuuri keskimääräisestä neliöerosta kunkin yksittäisen luvun ja näiden lukujen keskiarvon välillä.
Tärkeää on, että tämä kaava olettaa aineistosi sisältävän koko kiinnostavan populaation (siksi ”populaatiokaava”). Jos aineistosi sisältää vain otoksen kohdejoukosta, katso alla.
Populaatiokaava – Ohjelmistot
Voit käyttää tätä kaavaa Google sheetsissä, OpenOfficessa ja Excelissä kirjoittamalla =STDEVP(...) soluun. Määritä sulkujen väliin numerot, joiden yli haluat keskihajonnan, ja paina Enter-näppäintä. Alla oleva kuva havainnollistaa ideaa.
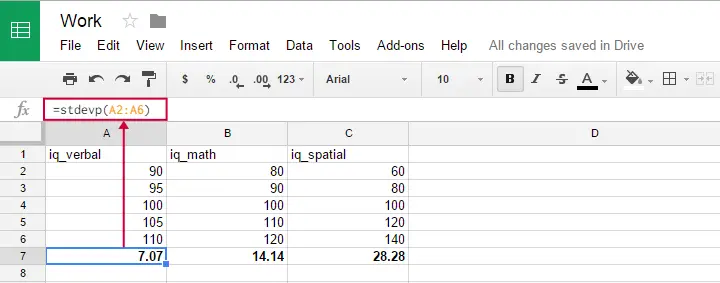
Kummallista kyllä, populaation keskihajonnan kaavaa ei näytä olevan olemassa SPSS:ssä.
Keskihajonta – otoksen kaava
Ja nyt jotain haastavaa: jos aineistosi on (suunnilleen) yksinkertainen satunnaisotos jostain (paljon) suuremmasta populaatiosta, edellinen kaava aliarvioi systemaattisesti tämän populaation keskihajonnan. Puolueeton estimaattori populaation keskihajonnalle saadaan käyttämällä
$$$S_x = \sqrt{\frac{\sum(X – \overline{X})^2}{N -1}}$$$
Laskutoimitusten osalta suuri ero ensimmäiseen kaavaan on se, että jaamme \(n -1\):llä \(n\):n sijaan. Jakamalla pienemmällä luvulla saadaan (hieman) suurempi tulos. Tämä kompensoi juuri edellä mainitun aliarvioinnin. Suurten otoskokojen tapauksessa näiden kahden kaavan tulokset ovat kuitenkin lähes identtiset.
GoogleSheetsissä, Open Officessa ja MS Excelissä STDEV-funktio käyttää tätä toista kaavaa. Se on myös (ainoa) SPSS:ssä toteutettu keskihajonnan kaava.
Keskihajonta ja varianssi
Toinen luku, joka ilmaisee, kuinka kaukana joukko lukuja on toisistaan, on varianssi. Varianssi on keskihajonnan neliö. Tästä seuraa, että samoin kuin keskihajonnalla, varianssilla on sekä populaatio- että otoskaava.
Periaatteessa on hankalaa, että kaksi eri tilastoa ilmaisevat periaatteessa saman ominaisuuden lukujoukosta. Miksi emme vain hylkää varianssia keskihajonnan hyväksi (tai päinvastoin)? Perusvastaus on, että keskihajonnalla on joissakin tilanteissa toivottavampia ominaisuuksia ja varianssilla toisissa.
