Kosinuksen samankaltaisuus ja kosinusetäisyys

Kosinusmaista samankaltaisuutta (cosinus similarity) käytetään dokumenttien tai vektoreiden välisen samankaltaisuuden määrittämiseen. Matemaattisesti se mittaa kahden moniulotteiseen avaruuteen projisoidun vektorin välisen kulman kosinia.Käytettävissä on muitakin samankaltaisuuden mittaustekniikoita, kuten euklidinen etäisyys tai Manhattanin etäisyys, mutta keskitymme tässä yhteydessä kosinin samankaltaisuuteen ja kosinietäisyyteen.

Kosinuksen samankaltaisuuden ja kosinusetäisyyden suhde voidaan määritellä seuraavasti.

1. Samankaltaisuus pienenee, kun kahden vektorin välinen etäisyys kasvaa

>2. Samankaltaisuus kasvaa, kun kahden vektorin välinen etäisyys pienenee.

Kosiinimäinen samankaltaisuus ja kosinimäinen etäisyys:

Kosiinimaisen samankaltaisuuden mukaan löytääkseen samankaltaisuuden kahden pisteen tai vektorin välille meidän on löydettävä niiden välille kulma.

Formula kosinuksen samankaltaisuuden ja etäisyyden löytämiseksi on seuraava:

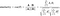
Tässä A= piste P1,B=Piste P2 (esimerkissämme)

Katsotaan Cos Θ:n eri arvoja, jotta ymmärretään kahden datapisteen (vektorin) P1 & P2 välinen kosinin samankaltaisuus ja kosinin etäisyys ottaen huomioon kaksi akselia X ja Y.

Alhaalla olevassa kuvassa on tapauksia.

Tapaus 1: Kun pisteiden P1 & P2 välinen kulma on 45 astetta, niin

cosine_similarity= Cos 45 = 0.525

Tapaus 2: Kun kaksi pistettä P1 & P2 ovat kaukana toisistaan ja pisteiden välinen kulma on 90 astetta niin

cosine_similarity= Cos 90 = 0

Tapaus 3:

Tapaus 4: Kun pisteet P1 & P2 sijaitsevat vastakkain ja pisteiden välinen kulma on 180 astetta, niin

kosiinimaisuus= Cos 180 = -1

Tapaus 5: Kun pisteiden P1 & P2 välinen kulma on 270 astetta, niin

kosiinimaisuus= Cos 270 = 0

Tapaus 6: Kun pisteiden P1 & P2 välinen kulma on 360 astetta, niin

cosine_similarity= Cos 360 = 1

Päästetään läpi nämä arvot kullekin kulmalle, joista on puhuttu edellä, ja tarkastellaan kosinusetäisyyksiä näiden kahden pisteen välillä.

1 – Cosine_Similarity=Cosine_Distance

Tapaus 1: Kun Cos 45 astetta

Vaihdetaan arvot yllä olevaan kaavaan .

1-0.525= Cosine_Distance

0.475 =Cosine_Distance

Tapaus 2: Kun Cos 90 astetta

1-0= Cosine_Distance

1 =Cosine_Distance

Tapaus 3: Kun Cos 0 astetta

1-1= Cosine_Distance

0 =Cosine_Distance

Tapaus 4: Kun Cos 180 astetta

1-(-1)= Kosinusetäisyys

2 =Kosinusetäisyys

Tapaus 5: Kun Cos 270 astetta

1-0= Kosinusetäisyys

1 =Kosinusetäisyys

Tapaus 6: Kun Cos 360 astetta

1-1= Cosine_Distance

0 =Cosine_Distance

Voidaan selvästi nähdä, että kun etäisyys on pienempi, samankaltaisuus on suurempi (pisteet ovat lähellä toisiaan) ja kun etäisyys on suurempi, kaksi pistettä ovat erisuuruisia (kaukana toisistaan)

Kosinuksen samankaltaisuutta ja kosinusetäisyyttä käytetään paljon suositusjärjestelmissä suosittelemaan tuotteita käyttäjille heidän mieltymystensä perusteella.

Vähäisiä esimerkkejä, joissa tätä käytetään, ovat verkkosivustot kuten Amazon, Flipkart suosittelemaan tuotteita asiakkaille henkilökohtaista kokemusta varten, elokuvien luokitus ja suosittelu jne.

Johtopäätös : Toivon, että nyt sinulla on selkeä käsitys matemaattisesta laskennasta kosinin samankaltaisuuden ja kosinin etäisyyden laskennan ja sen käytön takana.

Toivottavasti pidit artikkelistani.Paina taputusta 👏(50 kertaa) motivoidaksesi minua kirjoittamaan lisää.

Want to connect :

Linked In : https://www.linkedin.com/in/anjani-kumar-9b969a39/

Jos pidät postauksistani täällä Mediumissa ja haluaisit minun jatkavan tätä työtä, harkitse tukeasi patreonissa

.