Linkkitilan reititys on tekniikka, jossa kukin reititin jakaa tiedon naapurustostaan jokaiselle muulle internetverkon reitittimelle.
Linkkitilan reititysalgoritmin ymmärtämisen kolme avainta:
- Tieto naapurustosta: Reititystaulukkonsa lähettämisen sijasta reititin lähettää vain tiedon naapurustostaan. Reititin lähettää muille reitittimille suoraan liitettyjen linkkiensä tunnistetiedot ja kustannukset.
- Flooding: Kukin reititin lähettää tiedot jokaiselle muulle internetverkon reitittimelle paitsi naapureilleen. Tämä prosessi tunnetaan nimellä Flooding. Jokainen paketin vastaanottava reititin lähettää kopiot kaikille naapureilleen. Lopulta jokainen reititin saa kopion samasta tiedosta.
- Tiedon jakaminen: Reititin lähettää tiedon jokaiselle toiselle reitittimelle vain silloin, kun tiedoissa tapahtuu muutos.
Linkkitilan reitityksessä on kaksi vaihetta:
Luotettava tulviminen
- Alkutila: Jokainen solmu tietää naapuriensa kustannukset.
- Lopputila: Jokainen solmu tuntee koko graafin.
REITTIEN LASKEMINEN
Jokainen solmu käyttää Dijkstran algoritmia graafissa laskeakseen optimaaliset reitit kaikkiin solmuihin.
- Linkkitilan reititysalgoritmi tunnetaan myös nimellä Dijkstran algoritmi, jota käytetään löytämään lyhin polku yhdestä solmusta jokaiseen muuhun verkon solmuun.
- Dijkstran algoritmi on iteratiivinen, ja sillä on ominaisuus, että algoritmin k:nnen iteraation jälkeen pienimmän kustannuksen polut ovat hyvin tiedossa k:lle kohdesolmulle.
Kuvaillaan joitakin merkintöjä:
- c( i , j): Linkkikustannus solmusta i solmuun j. Jos solmut i ja j eivät ole suoraan yhteydessä toisiinsa, c(i , j) = ∞.
- D(v): Määrittää sen polun kustannukset lähdekoodista määränpäähän v, jolla on tällä hetkellä pienimmät kustannukset.
- P(v): Se määrittelee edellisen solmun (v:n naapuri) sekä nykyisen vähiten kustannuksia aiheuttavan polun lähteestä v:hen.
- N: Se on verkossa käytettävissä olevien solmujen kokonaismäärä.
Algoritmi
InitializationN = {A} // A is a root node.for all nodes vif v adjacent to Athen D(v) = c(A,v)else D(v) = infinityloopfind w not in N such that D(w) is a minimum.Add w to NUpdate D(v) for all v adjacent to w and not in N:D(v) = min(D(v) , D(w) + c(w,v))Until all nodes in N
Ylläolevassa algoritmissa alkutilannevaiheen jälkeen seuraa silmukka. Silmukan suorituskertojen määrä on yhtä suuri kuin verkossa käytettävissä olevien solmujen kokonaismäärä.
Ymmärretään esimerkin avulla:
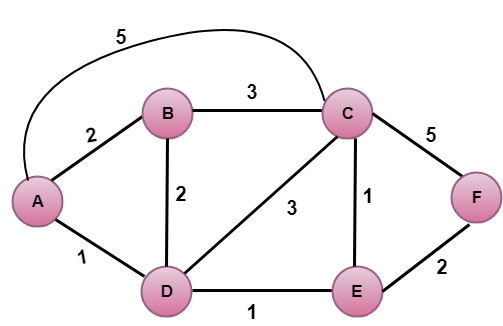
Yllä olevassa kuvassa lähdepiste on A.
Vaihe 1:
Ensimmäinen vaihe on alustusvaihe. Tällä hetkellä tiedossa oleva pienimmän kustannuksen polku A:sta suoraan siihen liitettyihin naapureihin B, C ja D on vastaavasti 2,5,1. Kustannus A:sta B:hen on 2, A:sta D:hen 1 ja A:sta C:hen 5. Kustannukset A:sta E:hen ja F:ään asetetaan äärettömiksi, koska ne eivät ole suoraan yhteydessä A:han.
| Step | N | D(B) | D(B) | D(C) | D(D) | D(D) | D(E) | D(F),P(F) |
|---|---|---|---|---|---|---|---|---|
| 1 | A | 2,A | 5,A | 1,A | ∞ | ∞ |
Vaihe 2:
Yllä olevasta taulukosta havaitaan, että piste D sisältää vähiten kustannuksia aiheuttavan polun vaiheessa 1. Siksi se lisätään N:ään. Nyt on määritettävä vähiten kustannuksia aiheuttava polku D-pisteen kautta.
a) Lyhimmän polun laskeminen A:sta B:hen
b) Lyhimmän polun laskeminen A:sta C:hen
c) Lyhimmän polun laskeminen A:sta E:hen
Huomautus: Piste D:llä ei ole suoraa linkkiä pisteeseen E. Siksi D(F):n arvoksi muodostuu ääretön arvoa D(F).
| Step | N | D(B),P(B) | D(C),P(C) | D(D),P(D) | D(E),P(E) | D(F),P(F) | |
|---|---|---|---|---|---|---|---|
| 1 | A | 2,A | 5,A | 1,A | ∞ | ∞ | |
| 2 | AD | 2,A | 4,D | 2,D | ∞ |
Vaihe 3:
Yllä olevasta taulukosta havaitaan, että sekä E:llä että B:llä on vähiten kustannuksia aiheuttava polku vaiheessa 2. Tarkastellaan E-pistettä. Määritellään nyt muiden kärkipisteiden vähimmän kustannuksen polku E:n kautta.
a) Lasketaan lyhin polku A:sta B:hen.
b) Lasketaan lyhin polku A:sta C:hen.
c) Lasketaan lyhin polku A:sta F:ään.
| Vaihe | N | D(B),P(B) | D(C),P(C) | D(D),P(D) | D(E),P(E) | D(F),P(F) | |
|---|---|---|---|---|---|---|---|
| 1 | A | 2,A | 5,A | 1,A | ∞ | ∞ | |
| 2 | AT | AD | 2,A | 4,D | 2,D | ∞ | |
| 3 | ADE | 2,A | 3,E | 3,E | 4,E |
Vaihe 4:
Yllä olevasta taulukosta havaitaan, että B-pisteellä on vähiten kustannuksia aiheuttava polku vaiheessa 3. Siksi se lisätään N:ään. Nyt määritetään jäljellä olevien kärkipisteiden pienimmän kustannuksen polku B:n kautta.
a) Lasketaan lyhin polku A:sta C:hen.
b) Lasketaan lyhin polku A:sta F:ään.
| Step | N | D(B),P(B) | D(C),P(C) | D(D),P(D) | D(E),P(E) | D(F),P(F) | |||
|---|---|---|---|---|---|---|---|---|---|
| 1 | A | 2,A | 5,A | 1,A | ∞ | ∞ | |||
| 2 | AD | 2,A | 4,D | 2,D | ∞ | ||||
| 3 | ADE | 2,A | 3,E | 3,E | 3,E | 2,D | 2,D | ∞ | |
| 3 | ADE | 3,E | 3,E | ||||||
| 4 | ADEB | 3,E | 4,E |
Vaihe 5:
Yllä olevasta taulukosta havaitaan, että C-pisteellä on vähiten kustannuksia aiheuttava polku vaiheessa 4. Siksi se lisätään N:ään. Nyt määritetään jäljelle jäävien kärkien pienimmän kustannuksen polku C:n kautta.
a) Lyhimmän polun laskeminen A:sta F:ään.
| Step | N | D(B),P(B) | D(C),P(C) | D(D),P(D) | D(E),P(E) | D(F),P(F) | |||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | A | 2,A | 5,A | 1,A | ∞ | ∞ | |||||||||||||||||||||||||||||
| 2 | AD | 2,A | 4,D | 2,D | ∞ | ||||||||||||||||||||||||||||||
| 3 | ADE | 2,A | 3,E | 4,E | |||||||||||||||||||||||||||||||
| 4 | ADEB | 3,
|
