Murtolukujen yhteenlasku (tai vähennyslasku) edellyttää, että murtolukujen nimittäjät ovat yhtä suuret.
Yhtäläiset nimittäjät
Jos nimittäjät ovat yhtä suuret, murtolukujen summa saadaan laskettua laskemalla yhteen nimittäjät ja pitämällä hallussaan nimittäjä.
Esimerkki:
Lisätään 4/7 ja 3/7:
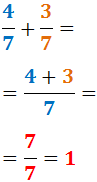 Samalla tavalla lasketaan yhtä suuren nimittäjän omaavien murtolukujen vähennyslasku vähentämällä osoittajat ja säilyttämällä nimittäjä.
Samalla tavalla lasketaan yhtä suuren nimittäjän omaavien murtolukujen vähennyslasku vähentämällä osoittajat ja säilyttämällä nimittäjä.
Esimerkki:
Vähennämme 4/7 ja 3/7:
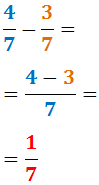
Eroavat nimittäjät
Kun nimittäjät ovat erilaiset, joudumme hieman operoimaan muuttaaksemme murtoluvut ekvivalenttisiksi murtoluvuiksi niin, että niillä on sama nimittäjä.
Kerrotaan menettely laskettaessa summaa
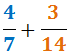
1. Laskemme nimittäjien pienimmän yhteisen kertaluvun:
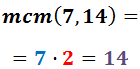
2. Laskemme nimittäjien pienimmän yhteisen kertaluvun. Kunkin murtoluvun nimittäjään kirjoitetaan saatu pienin yhteinen monikerta:
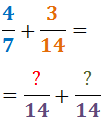
3. Kunkin murtoluvun osoittajaan kirjoitetaan tulos, joka saadaan jakamalla pienin yhteinen monikerta (uusi nimittäjä) alkuperäisellä nimittäjällä ja kertomalla se alkuperäisellä osoittajalla: Ensimmäisen murtoluvun alkuperäinen nimittäjä oli 7 ja alkuperäinen osoittaja oli 4:
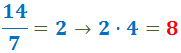
Toisen murtoluvun alkuperäinen nimittäjä oli 14 ja alkuperäinen osoittaja 3:
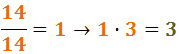
Siten saamme kahden yhtä suuren nimittäjän omaavan murtoluvun summan:
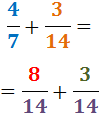
4. Laskemme murtoluvut yhteen:
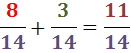
Vähentämiseksi noudatamme samoja vaiheita, mutta lopussa murtolukujen lisäämisen sijasta vähennämme ne.
Murtolukujen resurssit:
- Murtoluvun käsite
- Murtolukujen yksinkertaistaminen
- Yhtäläiset murtoluvut (1)
- Yhtäläiset murtoluvut (2)
- Murtolukujen yhteen- ja vähennyslasku
- Murtolukujen kertolasku ja jakolasku. Murtoluvut
- Murtolukuja tuottavat desimaaliluvut
- Sekamurtoluvut
- Prosenttiongelmat
- Interaktiiviset murtolukuharjoitukset
- Operaatiot murtoluvuilla
