Un écart-type est un nombre qui nous indique
dans quelle mesure un ensemble de nombres sont séparés.Un écart-type peut aller de 0 à l’infini. Un écart-type de 0 signifie qu’une liste de nombres sont tous égaux -ils ne sont pas du tout séparés.
Ecart-type – Exemple
Cinq candidats ont passé un test de QI dans le cadre d’une demande d’emploi. Leurs scores sur trois composantes du QI sont présentés ci-dessous.
Maintenant, examinons de près les scores sur les 3 composantes du QI. Notez que toutes les trois ont une moyenne de 100 sur nos 5 candidats. Cependant, les scores sur iq_verbal sont plus proches les uns des autres que les scores sur iq_math. En outre, les scores de la composante iq_spatiale sont plus éloignés que ceux des deux premières composantes. L’écart précis entre un certain nombre de scores peut être exprimé sous la forme d’un nombre. Ce nombre est connu sous le nom d’écart-type.
Écart-type – Résultats
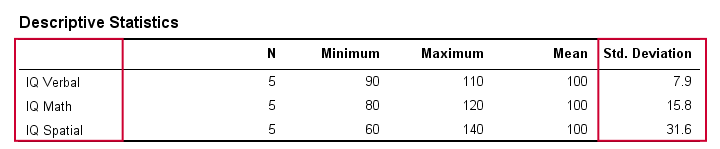
Dans la vie réelle, nous n’inspectons évidemment pas visuellement les scores bruts afin de voir à quel point ils sont éloignés les uns des autres. Au lieu de cela, nous allons simplement demander à un logiciel de les calculer pour nous (nous y reviendrons plus tard). Le tableau ci-dessous présente les écarts types et d’autres statistiques pour nos données de QI. Notez que les écarts types confirment le modèle que nous avons vu dans les données brutes.
Écart type et histogramme
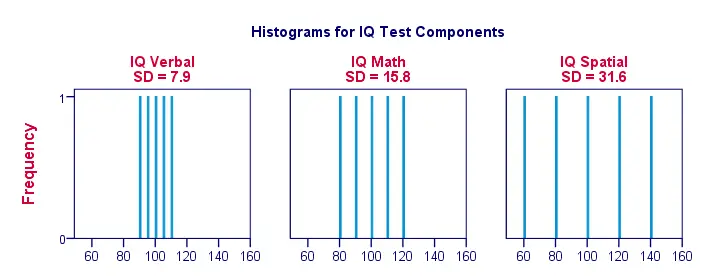
D’accord, rendons les choses un peu plus visuelles. La figure ci-dessous montre les écarts types et les histogrammes de nos scores de QI. Notez que chaque barre représente le score d’un candidat sur une composante du QI. Une fois de plus, nous voyons que les écarts types indiquent dans quelle mesure les scores sont éloignés les uns des autres.
Ecart type – Plus d’histogrammes
Lorsque nous visualisons des données sur une poignée d’observations seulement, comme dans la figure précédente, nous voyons facilement une image claire. Pour un exemple plus réaliste, nous allons présenter ci-dessous des histogrammes pour 1 000 observations. Il est important de noter que ces histogrammes ont des échelles identiques ; pour chaque histogramme, un centimètre sur l’axe des x correspond à environ 40 ‘points de composante du QI’.
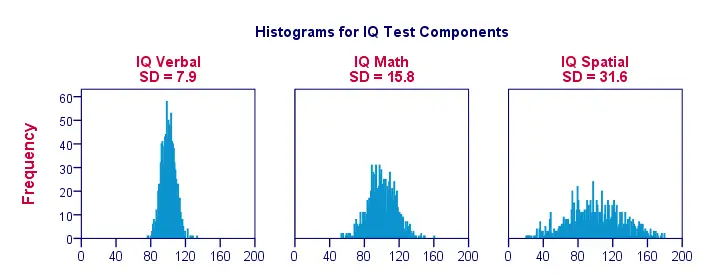
Notez comment les histogrammes permettent d’estimer grossièrement les écarts types. Des histogrammes » plus larges » indiquent des écarts types plus importants ; les scores (axe des x) sont plus éloignés les uns des autres. Comme tous les histogrammes ont des surfaces identiques (correspondant à 1 000 observations), des écarts types plus élevés sont également associés à des histogrammes ‘plus bas’.
Ecart type – Formule de la population
Alors, comment votre logiciel calcule-t-il les écarts types ? Eh bien, la formule de base est
$\sigma = \sqrt{\frac{\sum(X – \mu)^2}{N}}$
où
- \(X\) désigne chaque nombre distinct ;
- \(\mu\) désigne la moyenne sur tous les nombres et
- \(\sum\) désigne une somme.
En d’autres termes, l’écart type est la racine carrée de la différence quadratique moyenne entre chaque nombre individuel et la moyenne de ces nombres.
Important, cette formule suppose que vos données contiennent la totalité de la population d’intérêt (d’où « formule de population »). Si vos données ne contiennent qu’un échantillon de votre population cible, voir ci-dessous.
Formule de population – Logiciel
Vous pouvez utiliser cette formule dans Google sheets, OpenOffice et Excel en tapant =STDEVP(...) dans une cellule. Précisez les nombres sur lesquels vous souhaitez obtenir l’écart type entre les parenthèses et appuyez sur la touche Entrée. La figure ci-dessous illustre l’idée.
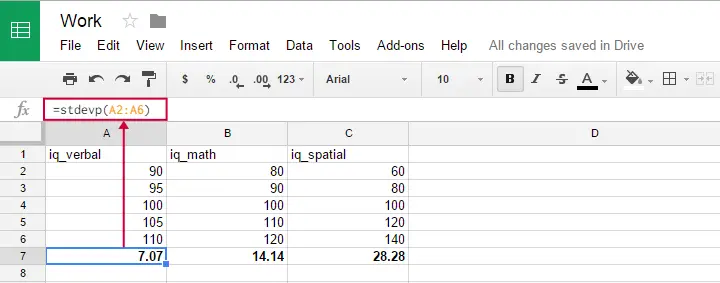
Oddly, la formule d’écart type de population ne semble pas exister dans SPSS.
Ecart type – Formule d’échantillon
Maintenant pour quelque chose de difficile : si vos données sont (approximativement) un simple échantillon aléatoire d’une certaine population (beaucoup) plus grande, alors la formule précédente sous-estimera systématiquement l’écart type dans cette population. Un estimateur sans biais de l’écart-type de la population est obtenu en utilisant
$S_x = \sqrt{\frac{\sum(X – \overline{X})^2}{N -1}}$
En ce qui concerne les calculs, la grande différence avec la première formule est que nous divisons par \(n -1\) au lieu de \(n\). En divisant par un nombre plus petit, on obtient un résultat (légèrement) plus grand. Cela compense précisément la sous-estimation susmentionnée. Pour les échantillons de grande taille, cependant, les deux formules ont des résultats pratiquement identiques.
Dans GoogleSheets, Open Office et MS Excel, la fonction STDEV utilise cette deuxième formule. C’est également la (seule) formule d’écart-type implémentée dans SPSS.
Ecart-type et variance
Un deuxième nombre qui exprime la distance entre un ensemble de nombres est la variance. La variance est l’écart-type au carré. Cela implique que, de la même manière que l’écart-type, la variance a une formule de population ainsi qu’une formule d’échantillon.
En principe, il est maladroit que deux statistiques différentes expriment fondamentalement la même propriété d’un ensemble de nombres. Pourquoi ne pas simplement écarter la variance au profit de l’écart-type (ou inversement) ? La réponse de base est que l’écart-type a des propriétés plus souhaitables dans certaines situations et la variance dans d’autres.
