Application du théorème de Buckingham Pi

Suivant : Importance des nombres non dimensionnels Up : Théorème de Buckingham Pi Previous : Théorème de Buckingham Pi

Application du théorème de Buckingham Pi

Le théorème que nous avons énoncé est très général, mais ne se limite nullement à la mécanique des fluides. Il est utilisé dans des domaines diversifiés tels que la botanique et les sciences sociales et des livres et volumes ont été écrits sur ce sujet. Mais nous n’avons pas besoin de beaucoup de théorie pour être en mesure de l’appliquer. Ce que nous allons considérer est une procédure pour utiliser le théorème et arriver à des nombres non dimensionnels pour un écoulement donné.

1. Listez toutes les variables qui régissent le processus. Ces variables doivent être indépendantes les unes des autres. Par exemple, on ne devrait pas choisir la densité, la gravité et le poids spécifique. La densité et le poids spécifique devraient faire l’affaire. Pour notre problème, nous avons F, D, V, et . Nous avons n = 5.
2. Marque les variables répétitives. Dans notre cas, ce sont D, V et ce qui donne k = 3.
3. Décidez combien de nombres non dimensionnels il y a. Dans notre cas, nous avons n – k = 2. Notre problème a 2 nombres non dimensionnels, et .
4. Définir les nombres non dimensionnels en regroupant les variables en n – k groupes de sorte que chaque groupe ait toutes les variables répétitives et une variable non répétitive. Ainsi, pour notre problème, nous avons

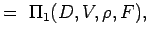
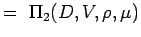
   		(5.2)
   Let
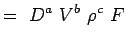
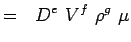
   		(5.3)

5. Exprimez maintenant chaque variable en fonction de ses dimensions. Utilisons le système MLT selon lequel les variables de nos problèmes ont les dimensions suivantes.
   

   Variable	Dimensions
   F, Force	M L / T2 ou M L T-2
   D, Diamètre :	L
   V, Vélocité	L/T ou LT-1
   , Densité :	M/L3 ou ML-3
   , Viscosité	ML-1T-1

   Substituant ces dimensions dans l’équation. 5.2, nous avons

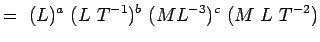
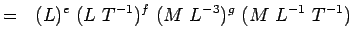
   		(5.4)
   Or
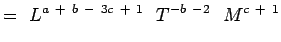
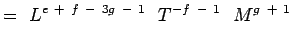
   		(5.5)

   Notant que et sont non dimensionnels, nous avons,

   a + b – 3c + 1 = 0 ; -b – 2 = 0, c + 1 = 0
   e + f – 3g – 1 = 0 ; -f – 1 = 0;g + 1 = 0	(5.6)

   La résolution des équations donne,

   a = -2, b = -2, c = -1
   e = -1, f = -1, g = -1	(5.7)

   Maintenant nos nombres non dimensionnels deviennent,

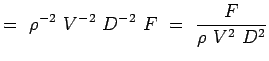
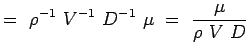
   		(5.8)

Nous avons donc trouvé les nombres non dimensionnels pour le flux qui nous intéresse, à savoir la traînée autour d’un cylindre circulaire. La relation fonctionnelle entre les deux nombres peut être exprimée comme suit

Mais notez que la forme du terme que nous avons dérivé est quelque peu différente de celle que nous avons supposée au début. Le côté droit de l’équation est en fait l’inverse du nombre de Reynolds ! Cela montre l’inconvénient de l’analyse, à savoir que la forme fonctionnelle exacte entre les nombres ne peut être obtenue. Tout coefficient ou indice obtenu ne peut être déterminé par cette analyse. Cela devrait être déterminé par l’expérimentation ou par des calculs. Mais puisque les nombres sont non dimensionnels, nous pouvons écrire,

Suivant : Importance des nombres non dimensionnels Up : Théorème de Buckingham Pi Previous : Théorème de Buckingham Pi

(c) Aerospace, Mechanical & Mechatronic Engg. 2005
Université de Sydney
.