Introduction :
La similarité cosinus est utilisée pour déterminer la similarité entre des documents ou des vecteurs. Mathématiquement, elle mesure le cosinus de l’angle entre deux vecteurs projetés dans un espace multidimensionnel.Il existe d’autres techniques de mesure de la similarité comme la distance euclidienne ou la distance de Manhattan disponibles, mais nous allons nous concentrer ici sur la similarité et la distance cosinus.
La relation entre la similarité cosinus et la distance cosinus peut être définie comme suit.
- La similarité diminue lorsque la distance entre deux vecteurs augmente

2. La similarité augmente lorsque la distance entre deux vecteurs diminue.

Cosinus de similarité et Cosinus de distance:
Le cosinus de similarité dit que pour trouver la similarité entre deux points ou vecteurs nous devons trouver l’Angle entre eux.
La formule pour trouver la similitude et la distance cosinus est la suivante :


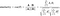
Ici A=Point P1,B=Point P2 (dans notre exemple)
Voyons les différentes valeurs de Cos Θ pour comprendre la similarité cosinus et la distance cosinus entre deux points de données(vecteurs) P1 & P2 en considérant deux axes X et Y.
L’image ci-dessous ayant là des cas.
Cas 1 : Lorsque l’angle entre les points P1 & P2 est de 45 degrés alors
cosine_similarité= Cos 45 = 0.525
Cas 2 : Lorsque deux points P1 & P2 sont éloignés l’un de l’autre et que l’angle entre les points est de 90 Degrés alors
cosine_similarité= Cos 90 = 0
Cas 3 : Lorsque deux points P1 & P2 sont très proches et se trouvent sur le même axe l’un par rapport à l’autre et l’angle entre les points est de 0 degré alors
cosine_similarité= Cos 0 = 1

L’image ci-dessous présentant les trois cas suivants.
Cas 4 : Lorsque les points P1 & P2 sont opposés l’un à l’autre et que l’angle entre les points est de 180 degrés alors
cosine_similarité= Cos 180 = -1
Cas 5 : Lorsque l’angle entre les points P1 & P2 est de 270 degrés alors
cosine_similarité= Cos 270 = 0
Cas 6 : Lorsque l’angle entre les points P1 & P2 est de 360 Degrés alors
cosine_similarité= Cos 360 = 1

Passons ces valeurs de chaque angles discutés ci-dessus et voyons la Distance Cosinus entre deux points.
1 – Cosinus_Similarité=Cosinus_Distance
Cas 1 : Quand Cos 45 Degré
Remplaçons les valeurs dans la formule ci-dessus .
1-0.525=Distance_cosinus
0.475 =Cosine_Distance
Cas 2 : Quand Cos 90 Degré
1-0= Cosine_Distance
1 =Cosine_Distance
Cas 3 : Quand Cos 0 Degré
1-1= Cosine_Distance
0 =Cosine_Distance
Cas 4 : Lorsque Cos 180 Degré
1-(-1)= Cosine_Distance
2 =Cosine_Distance
Cas 5 : Lorsque Cos 270 Degré
1-0= Cosine_Distance
1 =Cosine_Distance
Cas 6 : Quand Cos 360 Degré
1-1= Cosine_Distance
0 =Cosine_Distance
Nous pouvons clairement voir que lorsque la distance est moindre la similarité est plus grande(les points sont proches les uns des autres) et la distance est plus grande ,deux points sont dissemblables (éloignés les uns des autres)
Cosine Similitude et Cosine Distance est fortement utilisé dans les systèmes de recommandation pour recommander des produits aux utilisateurs en fonction de leurs goûts et dégoûts.
Peu d’exemples où cela est utilisé sont des sites web comme Amazon, Flipkart pour recommander des articles aux clients pour une expérience personnalisée, l’évaluation et la recommandation de films, etc.
Conclusion : J’espère que maintenant vous avez une compréhension claire des mathématiques derrière le calcul de la similarité cosinus et de la distance cosinus et de son utilisation.
J’espère que vous aimez mon article.S’il vous plaît frappez Clap 👏(50 fois) pour me motiver à écrire plus loin.
Vous voulez vous connecter :
Linked In : https://www.linkedin.com/in/anjani-kumar-9b969a39/
Si vous aimez mes posts ici sur Medium et que vous souhaitez que je continue à faire ce travail, pensez à me soutenir sur patreon
.
