L’estimation du temps, des efforts et du coût est l’une des parties les plus critiques de la gestion de projet. Cela est dû à l’importance fondamentale de ces estimations pour l’ensemble de la planification du projet et, en particulier, pour la portée, le calendrier et la base de coûts. L’une des techniques d’estimation suggérées dans le PMI Project Management Body of Knowledge (PMBOK 6th ed., ch. 6.4, 7.2) est l’estimation en trois points utilisée avec la distribution triangulaire, Beta ou PERT. Nous allons présenter ces méthodes dans cet article.
Qu’est-ce que la technique d’estimation en trois points ?
L’estimation en trois points est une approche simple mais utile pour estimer le temps ou le coût des éléments de travail. Selon la méthodologie du PMI, elle est utilisée dans les groupes de processus « Estimer la durée de l’activité » et « Estimer les coûts ». La technique implique trois estimations différentes qui sont généralement obtenues auprès d’experts en la matière :
- Estimation optimiste,
- Estimation pessimiste,
- Estimation la plus probable.
L’estimation optimiste est la quantité attendue de travail ou de temps nécessaire pour réaliser une activité en supposant qu’aucun obstacle ne survient et que tout se déroule sans problème. Elle représente ce que l’on appelle le meilleur scénario. Le point pessimiste est basé sur l’hypothèse que le contraire est vrai – il représente le pire scénario. Bien que les deux estimations se réfèrent aux points extrêmes de la gamme des résultats attendus, les estimations sont censées être quelque peu réalistes.
Le troisième point reflète le cas le plus probable, c’est l’estimation du travail ou du temps qui est jugée la plus réaliste. On pourrait être tenté d’utiliser simplement la moyenne entre les points optimiste et pessimiste sans y réfléchir à deux fois. Cependant, cela peut ne pas être approprié dans de nombreux cas. En pratique, il vaut normalement la peine de déterminer correctement cette estimation la plus probable, par analogie avec les autres points d’estimation.
Le résultat de l’estimation en trois points est une distribution dite triangulaire des valeurs de temps ou des montants de coûts, comprenant les trois estimations (voir l’illustration ci-dessous).
Qu’est-ce que PERT ?
PERT est l’acronyme de Program Evaluation and Review Technique et a été développé comme un système avancé de planification et de gestion du calendrier de projet par la marine américaine dans les années 1950 (source : Heldman, PMP Study guide, ch. 4).
Une autre histoire, pas trop sérieuse, de son origine a été publiée une fois par un auteur anonyme dans le journal du PMI (Link ; source : Anonyme (1975). PERT – le canular du siècle. Project Management Quarterly, 6(3), 22-23).
Dans les projets de style PMI, le PERT est principalement utilisé comme technique complémentaire à la méthode du chemin critique pour l’ordonnancement des activités. Cependant, il peut également être appliqué à des estimations autonomes des éléments de travail et des activités.
La distribution dite PERT s’appuie sur les valeurs déterminées avec la technique d’estimation à trois points. Elle peut fondamentalement être utilisée pour tous les niveaux de planification, allant des activités aux projets entiers. Cependant, trouver la bonne granularité pour une estimation significative peut nécessiter une réflexion critique et conceptuelle.
La méthode PERT implique de surpondérer l’estimation « la plus probable ». Elle transforme l’estimation à trois points en une courbe en forme de cloche et permet de déterminer les probabilités des plages de valeurs attendues.
Quelles sont les différences entre la distribution triangulaire et la distribution PERT des estimations à trois points ?
Alors que la distribution triangulaire ne prend en compte que les trois points estimés, la méthode PERT permet de convertir l’estimation à trois points en une courbe en forme de cloche, presque normalement distribuée.Ainsi, elle peut être utilisée pour le calcul des probabilités des plages de durées attendues.
Le diagramme suivant illustre les différences entre la distribution PERT, la distribution triangulaire et une représentation de l’estimation à trois points comme s’il s’agissait d’une distribution normale.
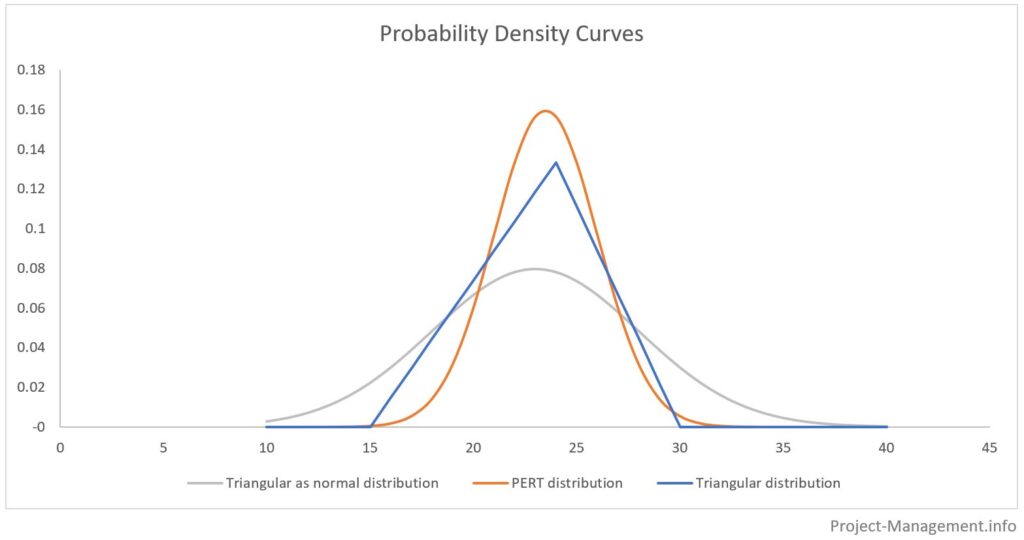
Les zones sous les courbes de distribution de probabilité représentent les probabilités cumulatives des plages d’estimations respectives. Généralement, ces plages sont déterminées avec la valeur attendue +/- l’écart type multiplié par 1, 2 et 3. Ceci est illustré dans la figure suivante:
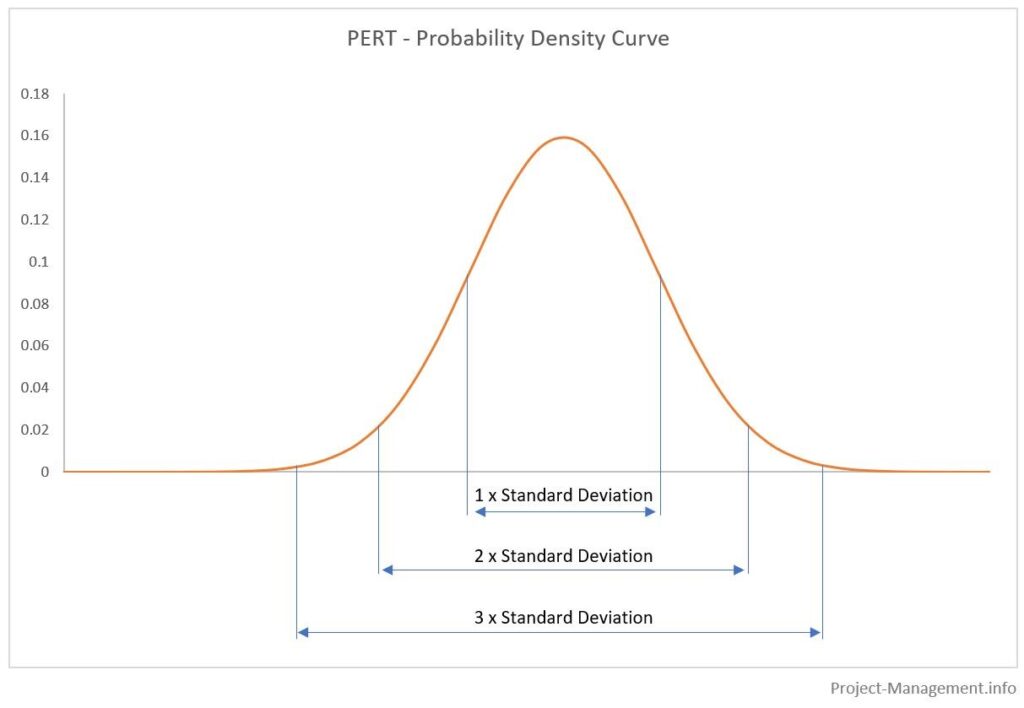
Les probabilités résultantes (approximativement) sont
- 68,3% pour 1 écart type,
- 95.5% pour 2 écarts types,
- 99,7% pour 3 écarts types.
Les connaissances requises pour l’examen PMP se limitent à calculer les estimations attendues et à connaître les différentes probabilités (source). Par conséquent, nous ne couvrirons pas les détails et le contexte statistiques dans cet article – vous pouvez trouver ces détails sur Riskamp.
Utilisez cette calculatrice pour déterminer les estimations à trois points et PERT.
Comment est calculée l’estimation à trois points ?
La distribution triangulaire
Le calcul simple mais couramment utilisé implique la moyenne ou la moyenne des 3 valeurs estimées. La formule de cette distribution triangulaire est :
E =(O + M + P) / 3
où :
E = montant attendu du temps ou du coût,
O = estimation optimiste,
M = estimation la plus probable,
P = estimation pessimiste.
Le PMBOK utilise t(E), t(O), t(M) et t(P) comme variables pour les estimations de temps et c(E), c(O), c(M) et c(P).
Le poids de chaque estimation dans cette équation est identique. Ainsi, le cas » le plus probable » n’affecte pas plus l’estimation finale que les 2 estimations moins probables. Ceci est différent de la méthode de la distribution bêta.
La distribution bêta de PERT
La distribution bêta de PERT tient compte du fait que le cas ‘le plus probable’ est plus susceptible de se produire, ce qui se reflète dans un multiplicateur pour cette estimation. La méthodologie PMI suggère ce calcul comme une alternative à la distribution triangulaire pour les estimations de coûts (cependant,nous sommes d’avis qu’elle peut également être utilisée pour les estimations de temps).
Dans cette méthode, l’estimation la plus probable reçoit un multiplicateur de 4 tandis que le diviseur global est porté à 6. Laformule est la suivante :
E =(O + 4*M + P) / 6
où :
E = montant attendu du temps ou du coût,
O = estimation optimiste,
M = estimation la plus probable,
P = estimation pessimiste.
L’écart-type de la distribution PERT est calculé à l’aide de la formule :
Ecart-type = (P – O) / 6
Pour l’estimation d’un chemin entier (méthode analogique du chemin critique), un concept similaire est appliqué mais en utilisant un écart-type combiné de toutes les activités.
Exemple d’une estimation en trois points et de PERT
Une équipe d’experts en la matière estime le temps nécessaire à la réalisation d’une activité. Dans cet exemple, la durée d’une activité est estimée à l’aide de la technique d’estimation en trois points.Ils obtiennent les chiffres suivants :
| Estimation optimiste | 15 jours |
| Estimation pessimiste | 24 jours |
| Estimation la plus probable | 30 jours |
Les valeurs vont de 15 jours (optimiste)à 30 jours (pessimiste). Une durée de 24 jours est considérée comme la durée la plus probable nécessaire à l’achèvement des travaux.
Calcul de la durée prévue avec une distribution triangulaire
La durée prévue à l’aide d’une distribution triangulaire est calculée comme suit :
Estimation finale = (15 + 30 + 24) / 3.
L’estimation finale qui en résulte selon cette méthode est de 23, ce qui est essentiellement la moyenne non pondérée des 3 estimations.
Calcul de la durée prévue à l’aide de la distribution bêta de PERT
La durée prévue peut également être calculée avec la méthode PERT :
Estimation finale (valeur prévue) = (15 + 4×24 + 30) / 6,
La valeur prévue résultante est de 23,5 jours, ce qui est supérieur à l’estimation finale déterminée selon la méthode triangulaire. Cela est dû au poids plus élevé (c’est-à-dire au multiplicateur de 4) qui est attribué à l’estimation « la plus probable ».
L’écart type de cette estimation est :
Ecart type = (30 – 15) / 6 = 2,5
Détermination des probabilités de la durée attendue
Après avoir calculé la durée attendue et l’écart type, le chef de projet peut déterminer les probabilités (approximatives.):
| Plage | Probabilité | Limite inférieure | Limite supérieure |
| 1 x écart-type | 68.3% | 21 | 26 |
| 2 x écart-type | 95.5% | 18,5 | 28,5 |
| 3 x écart-type | 99.7% | 16 | 31 |
Avec une probabilité de 68,3%, la durée de l’activité sera comprise entre 21 et 26 jours. Pour une fourchette de 18,5 à 28,5 jours, laprobabilité est de 95,5%. L’utilisation de 3 écarts types couvre la quasi-totalité de tous les points de données et détermine une probabilité de 99,7% que la durée sera finalement comprise entre 16 et 31 jours.
Sommaire
L’estimation finale selon la méthode triangulaire était de 23, contre 23,5 selon la méthode PERT. Cela s’explique par le fait que cette dernière attribue une pondération plus élevée au cas « le plus probable » qui, dans notre cas, n’est pas exactement la moyenne (ou la moyenne non pondérée) de l’estimation optimiste et de l’estimation pessimiste.
L’utilisation de la méthode PERT permet de prendre en compte les probabilités des plages de valeurs. Ceci est utile si la qualité des estimations varie, par exemple si la différence entre les estimations optimistes et pessimistes s’écarte de manière significative entre les différentes activités. Dans ce cas, l’utilisation des fourchettes et de leurs probabilités reflétera la dispersion et le niveau de confiance des estimations sous-jacentes.
Conclusion
L’estimation des activités par rapport à leurs exigences en matière de temps et de coûts est cruciale pour la planification et l’ordonnancement des projets et des activités. Dans de nombreux projets, des estimations plus précises, telles que les estimations paramétriques, basées sur des corrélations statistiques de projets comparables dans le passé, par exemple, ne sont pas disponibles. La technique d’estimation en trois points offre une bonne approche pour traiter et équilibrer les estimations descendantes ou celles des experts en la matière dans de telles situations.
La distribution PERT est probablement la méthode la plus précise pour agréger ces cas les plus défavorables, les meilleurs et les plus probables en un seul chiffre (valeur attendue) ou en une gamme de valeurs. Grâce à l’utilisation de l’écart-type, elle tient compte à la fois des incertitudes inhérentes et de la dispersion potentielle des estimations.
C’est peut-être la raison pour laquelle PERT est encore une méthode courante dans l’estimation et l’ordonnancement des projets, bien qu’elle existe depuis quelques décennies et qu’elle aurait déjà pu être utilisée par nos grands-parents (s’ils avaient été chefs de projet).
.
