Un comparateur numérique de magnitude est un circuit combinatoire qui compare deux nombres numériques ou binaires afin de savoir si un nombre binaire est égal, inférieur ou supérieur à l’autre nombre binaire. On conçoit logiquement un circuit pour lequel on aura deux entrées une pour A et l’autre pour B et on aura trois bornes de sortie, une pour la condition A > B, une pour la condition A = B et une pour la condition A < B.
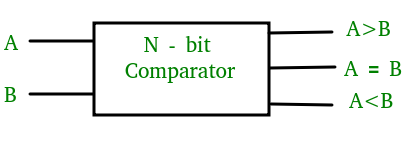
Comparateur d’amplitude à un bit –
Un comparateur utilisé pour comparer deux bits est appelé comparateur à un bit. Il est composé de deux entrées chacune pour deux nombres à un bit et de trois sorties pour générer un inférieur, un égal et un supérieur entre deux nombres binaires.
La table de vérité d’un comparateur à 1 bit est donnée ci-dessous :
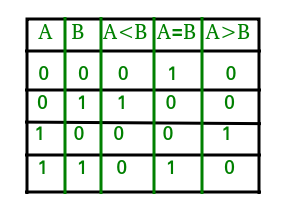
À partir de la table de vérité ci-dessus, les expressions logiques pour chaque sortie peuvent être exprimées comme suit :
A>B: AB'A<B: A'BA=B: A'B' + AB
À partir des expressions ci-dessus, nous pouvons dériver la formule suivante :

En utilisant ces expressions booléennes, nous pouvons mettre en œuvre un circuit logique pour ce comparateur comme indiqué ci-dessous :
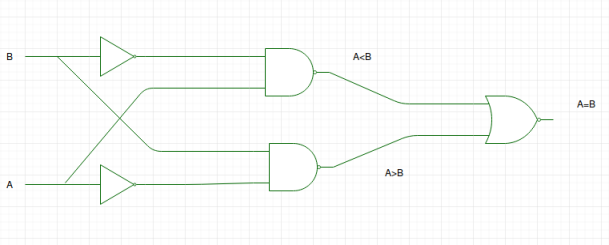
Le schéma logique est faux
Comparateur d’amplitude à 2 bits –
Un comparateur utilisé pour comparer deux nombres binaires de deux bits chacun est appelé comparateur d’amplitude à 2 bits. Il est composé de quatre entrées et de trois sorties pour générer des valeurs inférieures, égales et supérieures à entre deux nombres binaires.
La table de vérité d’un comparateur à 2 bits est donnée ci-dessous :
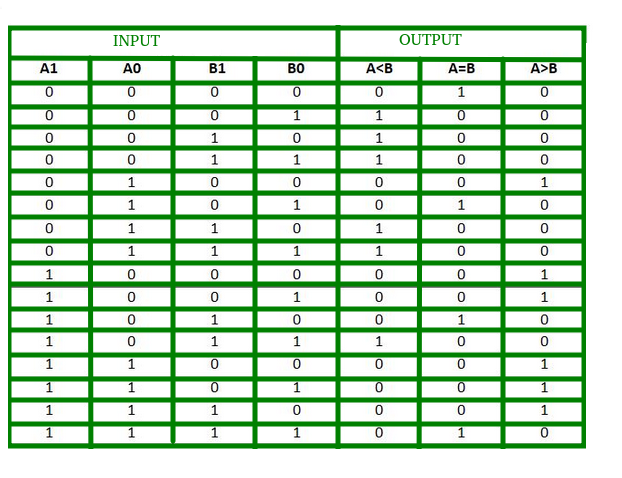
À partir de la table de vérité ci-dessus, la carte K pour chaque sortie peut être dessinée comme suit :



À partir des cartes K ci-dessus, les expressions logiques pour chaque sortie peuvent être exprimées comme suit :
A>B:A1B1' + A0B1'B0' + A1A0B0'A=B: A1'A0'B1'B0' + A1'A0B1'B0 + A1A0B1B0 + A1A0'B1B0' : A1'B1' (A0'B0' + A0B0) + A1B1 (A0B0 + A0'B0') : (A0B0 + A0'B0') (A1B1 + A1'B1') : (A0 Ex-Nor B0) (A1 Ex-Nor B1)A<B:A1'B1 + A0'B1B0 + A1'A0'B0
En utilisant ces expressions booléennes, nous pouvons mettre en œuvre un circuit logique pour ce comparateur comme indiqué ci-dessous :
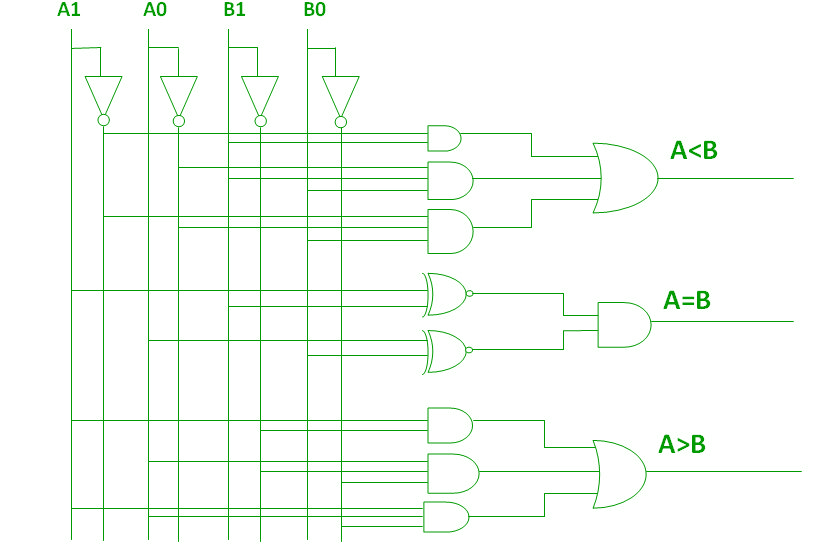
Comparateur d’amplitude à 4 bits –
Un comparateur utilisé pour comparer deux nombres binaires de quatre bits chacun est appelé comparateur d’amplitude à 4 bits. Il est composé de huit entrées chacune pour deux nombres de quatre bits et de trois sorties pour générer un inférieur, un égal et un supérieur entre deux nombres binaires.
Dans un comparateur à 4 bits, la condition de A>B peut être possible dans les quatre cas suivants :
- Si A3 = 1 et B3 = 0
- Si A3 = B3 et A2 = 1 et B2 = 0
- Si A3 = B3, A2 = B2 et A1 = 1 et B1 = 0
- Si A3 = B3, A2 = B2, A1 = B1 et A0 = 1 et B0 = 0
De même la condition pour A<B peut être possible dans les quatre cas suivants :
- Si A3 = 0 et B3 = 1
- Si A3 = B3 et A2 = 0 et B2 = 1
- Si A3 = B3, A2 = B2 et A1 = 0 et B1 = 1
- Si A3 = B3, A2 = B2, A1 = B1 et A0 = 0 et B0 = 1
La condition de A=B n’est possible que lorsque tous les bits individuels d’un nombre coïncident exactement avec les bits correspondants d’un autre nombre.
À partir des déclarations ci-dessus, les expressions logiques pour chaque sortie peuvent être exprimées comme suit :
AA, 831331 r : (A3 EioNor 33)A2132′ a (A3 Ex-Nor 133) (A2 Ex-Nor 132)A131′ a (A3 Ex-Nor 33) (A2 ENor132) (Al Ex-Nor 31)A01301
,13 : A3’03 a (A3 Ex-Nor 33)A211:12 a (A3 Ex-Nor 83) (A2 Ex-Nor 132)Ar131 a (A3 Ex-Nor 33) (A2 Ex-Nor32) (Al Ex-Nor 131)A0N30
A=B : (A3 Ex-Nor B3) (A2 Ex-Nor 82) (Al Ex-Nor BI) (AO Ex-Nor BO)
En utilisant ces expressions booléennes, nous pouvons mettre en œuvre un circuit logique pour ce comparateur comme indiqué ci-dessous :
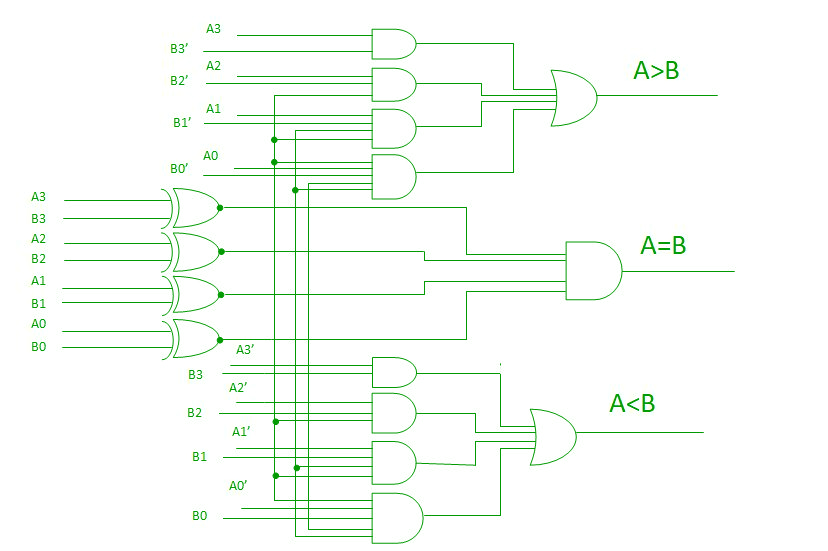
Comparateur en cascade –
Un comparateur effectuant l’opération de comparaison à plus de quatre bits en cascadant deux ou plusieurs comparateurs de 4 bits est appelé comparateur en cascade. Lorsque deux comparateurs doivent être mis en cascade, les sorties du comparateur d’ordre inférieur sont connectées aux entrées correspondantes du comparateur d’ordre supérieur.
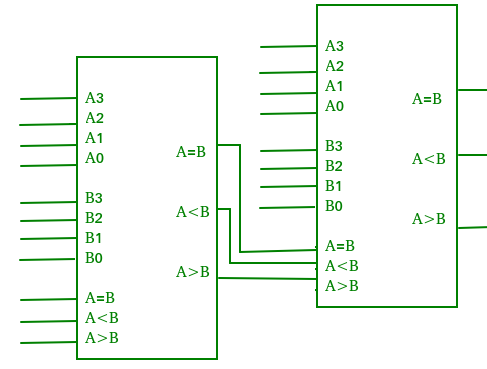
Applications des comparateurs –
- Les comparateurs sont utilisés dans les unités centrales de traitement (CPU) et les microcontrôleurs (MCU).
- Ils sont utilisés dans les applications de contrôle dans lesquelles les nombres binaires représentant des variables physiques telles que la température, la position, etc. sont comparés à une valeur de référence.
- Les comparateurs sont également utilisés comme contrôleurs de processus et pour la commande de servomoteurs.
- Utilisés dans la vérification de mots de passe et les applications biométriques.
