Il y a quelques années, Scott Fortmann-Roe a écrit un excellent essai intitulé « Comprendre le compromis biais-variance. »
Alors que la science des données se transforme en une profession acceptée avec son propre ensemble d’outils, de procédures, de flux de travail, etc, il semble souvent que l’on se concentre moins sur les processus statistiques en faveur des aspects plus excitants (voir ici et ici pour une paire d’exemples de discussions).
Définitions conceptuelles
Alors que ceci servira d’aperçu de l’essai de Scott, que vous pouvez lire pour plus de détails et d’aperçus mathématiques, nous commencerons par les définitions textuelles de Fortmann-Roe qui sont centrales à la pièce :
Erreur due au biais : L’erreur due au biais est prise comme la différence entre la prédiction attendue (ou moyenne) de notre modèle et la valeur correcte que nous essayons de prédire. Bien sûr, vous n’avez qu’un seul modèle, donc parler de valeurs de prédiction attendues ou moyennes peut sembler un peu étrange. Cependant, imaginez que vous puissiez répéter l’ensemble du processus de construction du modèle plusieurs fois : chaque fois que vous recueillez de nouvelles données et effectuez une nouvelle analyse, vous créez un nouveau modèle. En raison du caractère aléatoire des ensembles de données sous-jacents, les modèles résultants présenteront une gamme de prédictions. Le biais mesure à quel point les prédictions de ces modèles s’éloignent en général de la valeur correcte.
Erreur due à la variance : L’erreur due à la variance est prise comme la variabilité de la prédiction d’un modèle pour un point de données donné. Encore une fois, imaginez que vous pouvez répéter l’ensemble du processus de construction du modèle plusieurs fois. La variance est la mesure dans laquelle les prédictions pour un point donné varient entre différentes réalisations du modèle.
Essentiellement, le biais est la mesure dans laquelle les prédictions d’un modèle sont éloignées de l’exactitude, tandis que la variance est la mesure dans laquelle ces prédictions varient entre les itérations du modèle.
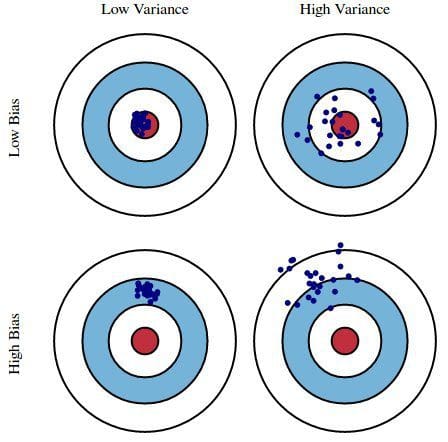
Fig. 1 : Illustration graphique du biais et de la variance
From Understanding the Bias-Variance Tradeoff, par Scott Fortmann-Roe.
Discussion
En prenant comme exemple un simple sondage défectueux sur l’élection présidentielle, les erreurs du sondage sont ensuite expliquées à travers les lentilles jumelles du biais et de la variance : la sélection des participants au sondage à partir d’un annuaire est une source de biais ; une petite taille d’échantillon est une source de variance ; la minimisation de l’erreur totale du modèle repose sur l’équilibrage des erreurs de biais et de variance.
Fortmann-Roe aborde ensuite ces questions dans le cadre d’un seul algorithme : k-Plus Proche Voisin. Il fournit ensuite quelques questions clés à prendre en compte lors de la gestion du biais et de la variance, y compris les techniques de ré-échantillonnage, les propriétés asymptotiques des algorithmes et leur effet sur les erreurs de biais et de variance, et la lutte contre les hypothèses de chacun vis-à-vis des données et de leur modélisation.
L’essai se termine en soutenant qu’au fond, ces 2 concepts sont étroitement liés à la fois au sur- et au sous-ajustement. À mon avis, voici le point le plus important :
A mesure que de plus en plus de paramètres sont ajoutés à un modèle, la complexité du modèle augmente et la variance devient notre principale préoccupation tandis que le biais diminue régulièrement. Par exemple, plus on ajoute de termes polynomiaux à une régression linéaire, plus la complexité du modèle résultant sera grande. En d’autres termes, le biais a une dérivée de premier ordre négative en réponse à la complexité du modèle tandis que la variance a une pente positive.

Fig. 2 : Biais et variance contribuant à l’erreur totale
From Understanding the Bias-Variance Tradeoff, par Scott Fortmann-Roe.
Fortmann-Roe termine la section sur le sur- et le sous-ajustement en pointant vers un autre de ses grands essais (Accurately Measuring Model Prediction Error), puis en passant à la recommandation hautement acceptable que « les mesures basées sur le rééchantillonnage telles que la validation croisée devraient être préférées aux mesures théoriques telles que le critère d’information d’Aikake. »
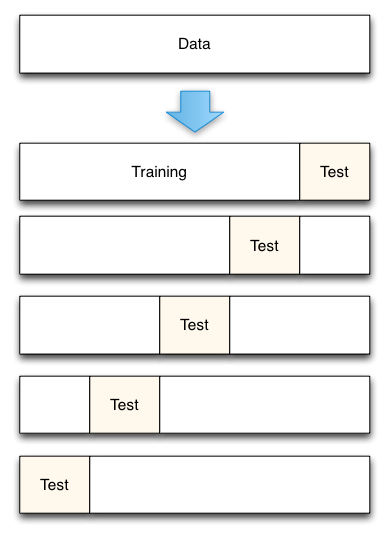
Fig. 3 : 5-Fold cross-validation data split
From Accurately Measuring Model Prediction Error, par Scott Fortmann-Roe.
Bien sûr, avec la validation croisée, le nombre de plis à utiliser (validation croisée à k plis, non ?), la valeur de k est une décision importante. Plus la valeur est faible, plus le biais dans les estimations d’erreur est élevé et moins la variance est importante. À l’inverse, lorsque k est égal au nombre d’instances, l’estimation de l’erreur est alors très peu biaisée mais peut présenter une variance élevée. Le compromis biais-variance est clairement important à comprendre, même pour la plus routinière des méthodes d’évaluation statistique, comme la validation croisée k-fold.
Malheureusement, la validation croisée semble aussi, parfois, avoir perdu son attrait dans l’ère moderne de la science des données, mais c’est une discussion pour une autre fois.
Je recommande de lire l’intégralité de l’essai de Scott Fortmann-Roe sur le compromis biais-variance, ainsi que son article sur la mesure de l’erreur de prédiction du modèle.
Relié:
- Big Data, Bible Codes, and Bonferroni
- Data Science of Variable Selection : Une revue
- Des ensembles de données sur les algorithmes
.
