C’est ce qu’on appelle parfois la théorie des marées « statiques », une théorie qui est apparue pour la première fois dans les célèbres Principia d’Isaac Newton. Après avoir identifié les forces qui produisent les marées, Newton, et d’autres qui l’ont suivi, ont imaginé un hypothétique océan mondial en équilibre statique avec ces forces – un équilibre nécessitant un sphéroïde d’eau aplati recouvrant la terre. « Prolétaire » signifie que la sphère en question a été étirée le long d’une ligne joignant deux pôles, non pas les pôles géographiques dans ce cas, mais les pôles en ligne avec le corps céleste (lune ou soleil), ce qui provoque la déformation de l’hypothétique sphère océanique. En jetant un autre coup d’œil au graphique illustrant les forces de traction dans le module précédent, on peut facilement imaginer l’eau convergeant vers ces pôles pour produire des « bourrelets de marée » jumeaux – des termes qui sont encore très populaires dans les manuels scolaires modernes.
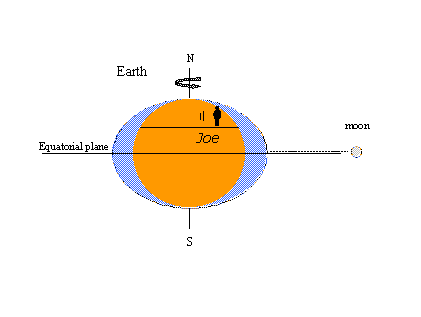
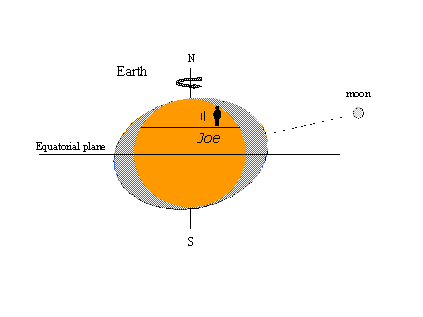
La raison de la popularité de la théorie de l’équilibre – le concept de bourrelets de marée au moins – est qu’il est facile d’expliquer certains phénomènes de marée bien connus avec des images. Dans l’image de gauche ci-dessous, un observateur imaginaire nommé Joe tourne avec la terre et rencontre les renflements statiques sous la forme de grandes marées. C’est à nouveau la marée haute douze heures lunaires plus tard, lorsque la lune traverse le méridien opposé de l’autre côté de la terre. Deux marées hautes et deux marées basses se produisent au cours d’un même jour lunaire qui dure 24 heures et 50 minutes en temps de montre (solaire). Dans la figure de droite, la lune a progressé dans son orbite autour de la terre jusqu’à une position au nord de l’équateur (déclinaison nord). Les bourrelets statiques se déplacent pour rester alignés avec la lune et Joe rencontre maintenant une inégalité diurne dans les marées hautes (marées hautes successives de hauteur inégale). La déclinaison lunaire maximale, au nord ou au sud de l’équateur, produit des marées tropicales ; les marées qui se produisent lorsque la lune est sur l’équateur sont appelées marées équatoriales. Les marées tropicales-équatoriales se reproduisent deux fois dans un intervalle de 27 1/3 jours – le mois tropique couvrant un cycle complet de la déclinaison lunaire. Toutes ces observations sont cohérentes avec la théorie de l’équilibre.
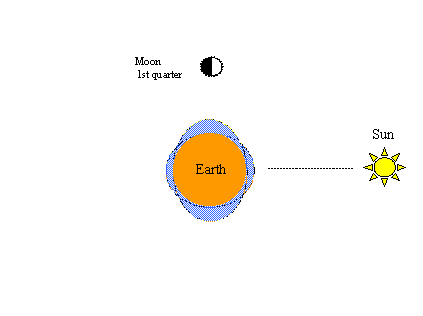
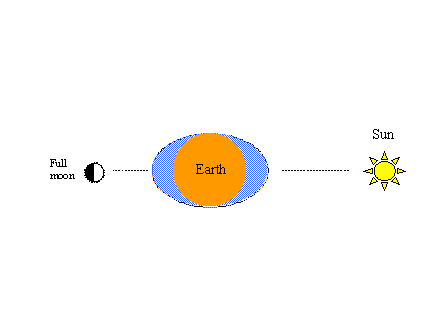
Un autre phénomène facile à démontrer de cette manière est le cycle bien connu du printemps et du coucher. La gravité solaire produit également une paire de renflements martiaux dans l’océan hypothétique. Lorsque les forces de traction du soleil et de la lune sont alignées, il en résulte des marées de printemps de plus grande amplitude (des hauts plus élevés et des bas plus bas), comme le montre la figure de gauche ci-dessous. Comme dans les figures précédentes, lorsque la lune complète un autre demi-cycle dans son orbite – cette fois de la pleine lune à la nouvelle lune – les marées de printemps se produiront à nouveau.
La figure ci-dessous à droite illustre la partie de mortes-eaux du cycle de printemps et de mortes-eaux ; c’est-à-dire que lorsque la lune est dans le premier quart (ou le troisième quart) de ce cycle, les forces de traction lunaire et solaire sont complètement désalignées, tendant à se contrecarrer l’une l’autre, et les marées de mortes-eaux de moindre amplitude (des hauts plus bas et des bas plus hauts) se produisent. Deux cycles de printemps et de mortes-eaux (deux printemps et deux mortes-eaux) sont accomplis en 29 ½ jours, soit la même période de temps nécessaire à la lune pour effectuer une orbite complète de la terre par rapport au soleil.
Les autres aspects de la marée observée en accord avec la théorie de l’équilibre comprennent le cycle périgéen-apogéen. Celui-ci découle du fait que l’orbite de la lune autour de la terre décrit une ellipse plutôt qu’un cercle. Les marées périgéniques de plus grande amplitude se produisent au périgée lunaire, lorsque la lune est la plus proche de la terre, et les marées apogéniques de moindre amplitude se produisent à l’apogée lunaire, lorsque la lune est la plus éloignée de la terre sur son orbite elliptique. Le cycle périgéen-apogéen prend environ 27 ½ jours pour se terminer.
Bien que la théorie de l’équilibre fasse un excellent travail d’explication des phénomènes cycliques de marée et des périodes de récurrence associées à beaucoup d’entre eux, c’est un exemple de modèle de comportement idéal – quelque chose qui fonctionne pour le but recherché bien qu’il puisse ne pas adhérer à la vérité dans toutes les circonstances. Nous n’avons pas besoin de chercher loin pour trouver ces exemples. La terre n’est que partiellement couverte par ses eaux, les masses terrestres empêchent tout ce qui ressemble à un abulge de voyager complètement autour d’elle, et les observations des marées réelles montrent qu’elles ne répondent pas instantanément aux forces de production de marée de la lune et du soleil comme la théorie l’exige.
