Le routage par état de liaison est une technique dans laquelle chaque routeur partage la connaissance de son voisinage avec tous les autres routeurs de l’interréseau.
Les trois clés pour comprendre l’algorithme de routage par état de liaison :
- Connaissance du voisinage : Au lieu d’envoyer sa table de routage, un routeur envoie les informations sur son voisinage seulement. Un routeur diffuse ses identités et le coût des liens directement attachés aux autres routeurs.
- Flooding : Chaque routeur envoie les informations à tous les autres routeurs de l’interréseau, à l’exception de ses voisins. Ce processus est connu sous le nom de Flooding. Chaque routeur qui reçoit le paquet envoie les copies à tous ses voisins. Finalement, chaque routeur reçoit une copie de la même information.
- Partage de l’information : Un routeur envoie l’information à chaque autre routeur seulement lorsque le changement se produit dans l’information.
Le routage par état de liaison a deux phases:
Flocage fiable
- Etat initial : Chaque nœud connaît le coût de ses voisins.
- État final : Chaque nœud connaît l’ensemble du graphe.
Calcul du routage
Chaque nœud utilise l’algorithme de Dijkstra sur le graphe pour calculer les routes optimales vers tous les nœuds.
- L’algorithme de routage par état de liaison est également connu sous le nom d’algorithme de Dijkstra qui est utilisé pour trouver le chemin le plus court d’un nœud à tous les autres nœuds du réseau.
- L’algorithme de Dijkstra est un itératif, et il a la propriété qu’après la kième itération de l’algorithme, les chemins de moindre coût sont bien connus pour k nœuds de destination.
Décrivons quelques notations:
- c( i , j) : Coût de liaison du nœud i au nœud j. Si les nœuds i et j ne sont pas directement liés, alors c(i , j) = ∞.
- D(v) : Il définit le coût du chemin du code source à la destination v qui a le moindre coût actuellement.
- P(v) : Il définit le nœud précédent (voisin de v) ainsi que le chemin actuel de moindre coût de la source à v.
- N : C’est le nombre total de nœuds disponibles dans le réseau.
Algorithme
InitializationN = {A} // A is a root node.for all nodes vif v adjacent to Athen D(v) = c(A,v)else D(v) = infinityloopfind w not in N such that D(w) is a minimum.Add w to NUpdate D(v) for all v adjacent to w and not in N:D(v) = min(D(v) , D(w) + c(w,v))Until all nodes in N
Dans l’algorithme ci-dessus, une étape d’initialisation est suivie par la boucle. Le nombre de fois que la boucle est exécutée est égal au nombre total de nœuds disponibles dans le réseau.
Comprenons par un exemple :
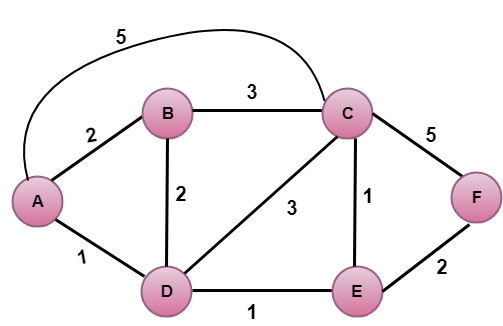
Dans la figure ci-dessus, le sommet source est A.
Etape 1:
La première étape est une étape d’initialisation. Le chemin de moindre coût actuellement connu de A vers ses voisins directement attachés, B, C, D sont respectivement 2,5,1. Le coût de A à B est fixé à 2, de A à D est fixé à 1 et de A à C est fixé à 5. Le coût de A vers E et F est fixé à l’infini car ils ne sont pas directement liés à A.
| Etape | N | D(B),P(B) | D(C),P(C) | D(D),P(D) | D(E),P(E) | D(F),P(F) |
|---|---|---|---|---|---|---|
| 1 | A | 2,A | 5,A | 1,A | ∞ | ∞ |
Etape 2 :
Dans le tableau ci-dessus, on observe que le sommet D contient le chemin de moindre coût à l’étape 1. Par conséquent, il est ajouté dans N. Maintenant, nous devons déterminer un chemin de moindre coût à travers le sommet D.
a) Calcul du plus court chemin de A à B
b) Calcul du plus court chemin de A à C
c) Calcul du plus court chemin de A à E
Note : Le sommet D n’a pas de lien direct avec le sommet E. Par conséquent, la valeur de D(F) est infinie.
| Etape | N | D(B),P(B) | D(C),P(C) | D(D),P(D) | D(E),P(E) | D(F),P(F) |
|---|---|---|---|---|---|---|
| 1 | A | 2,A | 5,A | 1,A | ∞ | ∞ |
| 2 | AD | 2,A | 4,D | 2,D | ∞ |
Etape 3 :
Dans le tableau ci-dessus, nous observons que E et B ont tous deux le chemin de moindre coût à l’étape 2. Considérons le sommet E. Maintenant, nous déterminons le chemin de moindre coût des sommets restants à travers E.
a) Calculer le chemin le plus court de A à B.
b) Calculer le chemin le plus court de A à C.
c) Calculer le chemin le plus court de A à F.
| Etape | N | D(B),P(B) | D(C),P(C) | D(D),P(D) | D(E),P(E) | D(F),P(F) |
|---|---|---|---|---|---|---|
| 1 | A | 2,A | 5,A | 1,A | ∞ | ∞ |
| 2 | AD | 2,A | 4,D | 2,D | ∞ | |
| 3 | ADE | 2,A | 3,E | 4,E |
Etape 4 :
Dans le tableau ci-dessus, on observe que le sommet B a le chemin de moindre coût à l’étape 3. Par conséquent, il est ajouté dans N. Maintenant, nous déterminons le chemin de moindre coût des sommets restants à travers B.
a) Calculer le chemin le plus court de A à C.
b) Calculer le chemin le plus court de A à F.
| Etape | N | D(B),P(B) | D(C),P(C) | D(D),P(D) | D(E),P(E) | D(F),P(F) | |
|---|---|---|---|---|---|---|---|
| 1 | A | 2,A | 5,A | 1,A | ∞ | ∞ | |
| 2 | AD | 2,A | 4,D | 2,D | ∞ | ||
| 3 | ADE | 2,A | 3,E | 4,E | |||
| 4 | ADEB | 3,E | 4,E |
Étape 5 :
Dans le tableau ci-dessus, on observe que le sommet C a le chemin de moindre coût à l’étape 4. Par conséquent, il est ajouté dans N. Maintenant, nous déterminons le chemin de moindre coût des sommets restants à travers C.
a) Calcul du plus court chemin de A à F.
| Etape | N | D(B),P(B) | D(C),P(C) | D(D),P(D) | D(E),P(E) | D(F),P(F) |
|---|---|---|---|---|---|---|
| 1 | A | 2,A | 5,A | 1,A | ∞ | ∞ |
| 2 | AD | 2,A | 4,D | 2,D | ∞ | |
| 3 | ADE | 2,A | 3,E | 4,E | ||
| 4 | ADEB | 3,E | 4,E | |||
| 5 | ADEBC | 4,E |
Tableau final :
| Etape | N | D(B),P(B) | D(C),P(C) | D(D),P(D) | D(E),P(E) | D(F),P(F) | |
|---|---|---|---|---|---|---|---|
| 1 | A | 2,A | 5,A | 1,A | ∞ | ∞ | |
| 2 | AD | 2,A | 4,D | 2,D | ∞ | ||
| 3 | ADE | 2,A | 3,E | 4,E | |||
| 4 | ADEB | 3,E | 4,E | ||||
| 5 | ADEBC | 4,E | |||||
| 6 | ADEBCF |
Avantage :
Un trafic important est créé dans le routage d’état de ligne en raison du Flooding. Le Flooding peut provoquer un bouclage infini, ce problème peut être résolu en utilisant le champ Time-to-leave
.
