En storleksjämförare är en kombinerad krets som jämför två digitala eller binära tal för att ta reda på om det ena binära talet är lika med, mindre än eller större än det andra binära talet. Vi utformar logiskt en krets för vilken vi kommer att ha två ingångar, en för A och en för B, och tre utgångsterminaler, en för A > B-tillstånd, en för A = B-tillstånd och en för A < B-tillstånd.
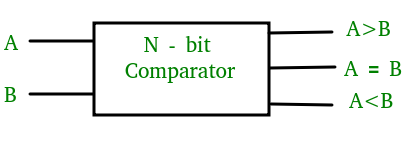
1-bitars magnitudkomparator –
En komparator som används för att jämföra två bitar kallas en enkelbitskomparator. Den består av två ingångar vardera för två enkelbitarstal och tre utgångar för att generera mindre än, lika med och större än mellan två binära tal.
Sanningstabellen för en 1-bitskomparator ges nedan:
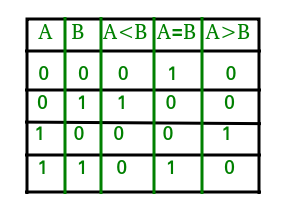
Från sanningstabellen ovan kan logiska uttryck för varje utgång uttryckas på följande sätt:
A>B: AB'A<B: A'BA=B: A'B' + AB
Från ovanstående uttryck kan vi härleda följande formel:

Med hjälp av dessa booleska uttryck kan vi implementera en logisk krets för denna komparator enligt nedan:
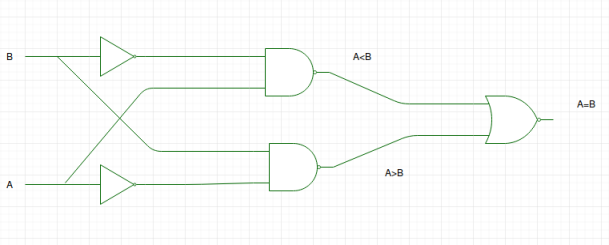
Logikdiagrammet är fel
2-bitars magnitudkomparator –
En komparator som används för att jämföra två binära tal med vardera två bitar kallas en 2-bitars magnitudkomparator. Den består av fyra ingångar och tre utgångar för att generera mindre än, lika med och större än mellan två binära tal.
Sanningstabellen för en 2-bitars komparator ges nedan:
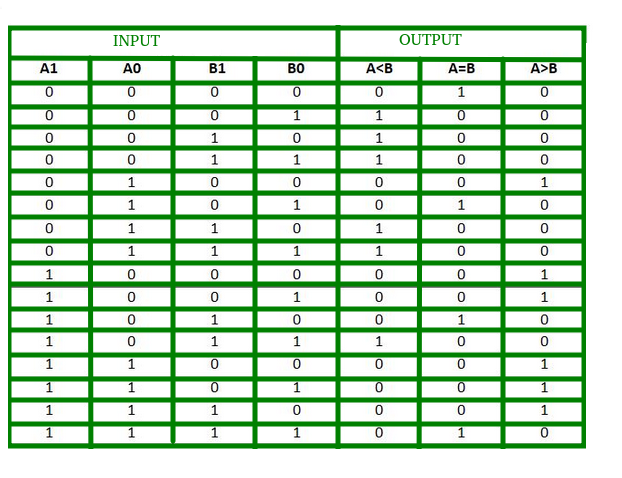
Från ovanstående sanningstabell kan K-map för varje utgång ritas på följande sätt:



Från ovanstående K-maps kan logiska uttryck för varje utgång uttryckas enligt följande:
A>B:A1B1' + A0B1'B0' + A1A0B0'A=B: A1'A0'B1'B0' + A1'A0B1'B0 + A1A0B1B0 + A1A0'B1B0' : A1'B1' (A0'B0' + A0B0) + A1B1 (A0B0 + A0'B0') : (A0B0 + A0'B0') (A1B1 + A1'B1') : (A0 Ex-Nor B0) (A1 Ex-Nor B1)A<B:A1'B1 + A0'B1B0 + A1'A0'B0
Med hjälp av dessa booleska uttryck kan vi implementera en logisk krets för denna komparator enligt nedan:
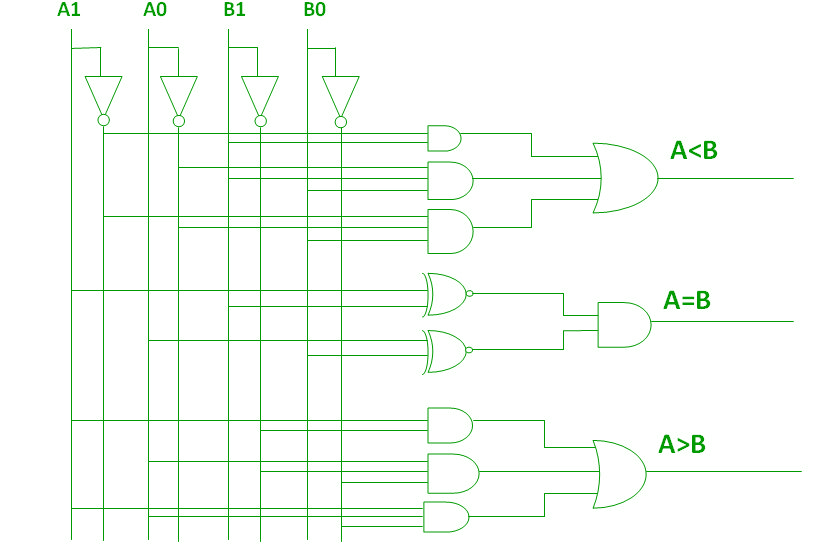
4-bitars magnitudkomparator –
En komparator som används för att jämföra två binära tal med vardera fyra bitar kallas 4-bitars magnitudkomparator. Den består av åtta ingångar vardera för två fyrbitarstal och tre utgångar för att generera mindre än, lika med och större än mellan två binära tal.
I en 4-bitars komparator kan tillståndet A>B vara möjligt i följande fyra fall:
- Om A3 = 1 och B3 = 0
- Om A3 = B3 och A2 = 1 och B2 = 0
- Om A3 = B3, A2 = B2 och A1 = 1 och B1 = 0
- Om A3 = B3, A2 = B2, A1 = B1 och A0 = 1 och B0 = 0
Samma villkor för A<B kan vara möjligt i följande fyra fall:
- Om A3 = 0 och B3 = 1
- Om A3 = B3 och A2 = 0 och B2 = 1
- Om A3 = B3, A2 = B2 och A1 = 0 och B1 = 1
- Om A3 = B3, A2 = B2, A1 = B1 och A0 = 0 och B0 = 1
Det är endast möjligt att ha villkoret A=B när alla enskilda bitar i ett tal exakt sammanfaller med motsvarande bitar i ett annat tal.
Från ovanstående uttalanden kan logiska uttryck för varje utgång uttryckas på följande sätt:
AA, 831331 r: (A3 EioNor 33)A2132′ a (A3 Ex-Nor 133) (A2 Ex-Nor 132)A131′ a (A3 Ex-Nor 33) (A2 ENor132) (Al Ex-Nor 31)A01301
,13: A3’03 a (A3 Ex-Nor 33)A211:12 a (A3 Ex-Nor 83) (A2 Ex-Nor 132)Ar131 a (A3 Ex-Nor 33) (A2 Ex-Nor32) (Al Ex-Nor 131)A0N30
A=B: (A3 Ex-Nor B3) (A2 Ex-Nor 82) (Al Ex-Nor BI) (AO Ex-Nor BO)
Med hjälp av dessa booleska uttryck kan vi implementera en logisk krets för denna komparator enligt nedan:
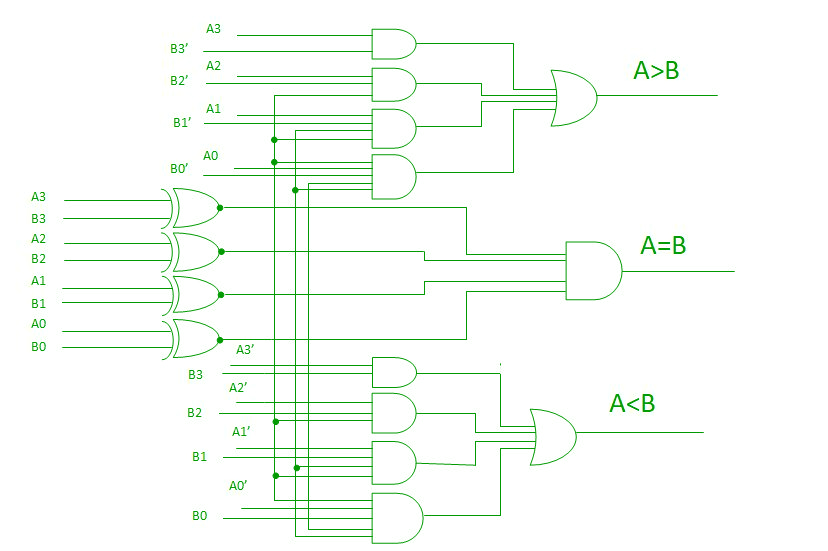
Kaskadkomparator –
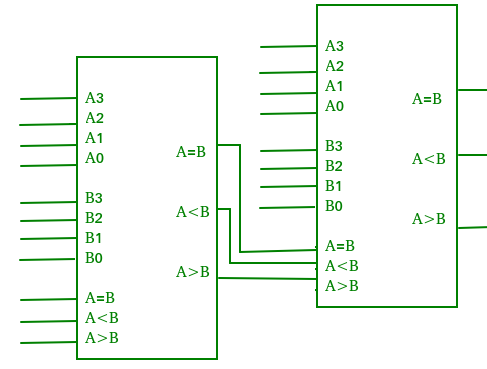
En komparator som utför jämförelseoperationen för mer än fyra bitar genom att kaskadera två eller flera 4-bitars komparatorer kallas kaskadkomparator. När två komparatorer ska kaskadkopplas ansluts utgångarna från den lägre komparatorn till motsvarande ingångar i den högre komparatorn.
Användningsområden för komparatorer –
- Komparatorer används i centrala processorer (CPU:er) och mikrokontroller (MCU:er).
- Dessa används i kontrolltillämpningar där de binära tal som representerar fysikaliska variabler, såsom temperatur, position osv. jämförs med ett referensvärde.
- Komparatorer används också som processkontroller och för styrning av servomotorer.
- Används vid verifiering av lösenord och biometriska tillämpningar.
