Next: 無次元数の重要性 Up: バッキンガム・パイ定理 Previous: バッキンガム・パイ定理
Application of Buckingham Pi theorem
ここで述べた定理は、非常に一般的ですが、決して流体力学に限ったことではありません。 植物学や社会科学など様々な分野で使われており、このテーマで書かれた本や冊子もある。 しかし、これを応用するために多くの理論は必要ない。 3613>
- プロセスを支配するすべての変数を列挙せよ。 これらの変数は互いに独立であるべきである。 例えば、密度、重力、比重を選ぶべきではない。 密度と比重で十分である。 この問題では、F、D、V、
、
があります。 n = 5. - 繰り返しの変数をマークする。 この場合、D、V、でk=3です。
- 無次元数はいくつあるか決めます。 我々の場合、n – k = 2 となる。 我々の問題では無次元数は2つ、
と
である。 - 無次元数を定義するには、変数をn – k個のグループに分け、各グループにすべての繰り返し変数と1つの非繰り返し変数があるようにする。 したがって我々の問題では
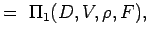
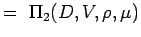
(5.2） Let
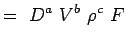
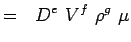
(5.5.X)3) - ここで、各変数を次元で表現する。 MLTシステムを用いると，我々の問題の変数は次の次元になる．
変数 次元 F、力 M L / T2またはM L T-2 D、直径 F、力
F、力。 L V, Velocity L/T or LT-1 、Density: M/L3 or ML-3 、粘度 ML-1T-1 これらの次元を式に代入すると、以下のようになる。 5.2より、
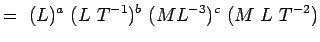
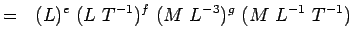
(5.) となる。4) Or
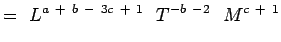
(5.0) ＜9866>(4)
＜4582>
(5.0)5) ここで、
とが無次元であることに注目すると、a + b – 3c + 1 = 0が得られる。 -b – 2 = 0, c + 1 = 0 e + f – 3g – 1 = 0; -f – 1 = 0; g + 1 = 0 (5.6) 方程式を解くと、
a = -2、b = -2、c = -1 e = -1、f = -1、g = -1 (5.7) ここで、我々の無次元数は、
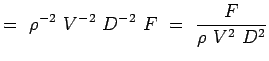
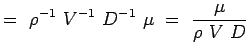
(5.8) こうして目的の流れ、すなわち円柱に対する抗力の無次元数を求めることができた。 この2つの数値の関数的な関係は
と表されるが、我々が導き出した項
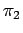の形は、最初に想定したものとは多少異なっていることに注意されたい。 式の右辺は実はレイノルズ数の逆数である！これは、
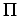数間の正確な関数形が得られないという解析の欠点を指摘している。 得られた係数や指標は、この解析で決定することはできない。 これは実験や計算によって決定されるべきものである。 しかし、この数は無次元であるから、
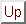
と書くことができる、次は、
と書く。 無次元数の重要性 Up: バッキンガム円周率定理 Previous: バッキンガム円周率定理(c) Aerospace, Mechanical & Mechatronic Enggs. 2005
シドニー大学
研究室