リンクステート ルーティングは、各ルータがその近隣の知識をインターネットワーク内の他のすべてのルータと共有する技術です。
リンクステート ルーティング アルゴリズムを理解するための3つの鍵:
- 近隣についての知識:ルーティング テーブルを送るのではなく、その近隣についての情報のみを送るルーターがある。 ルータは、直接接続されたリンクのアイデンティティとコストを他のルータにブロードキャストします。 各ルーターは、近隣のルーターを除く、インターネットネットワーク上の他のすべてのルーターに情報を送信します。 このプロセスは、フラッディングとして知られています。 パケットを受信したすべてのルータは、そのすべての隣人にコピーを送信します。 最後に、各ルーターは同じ情報のコピーを受け取ります。
- 情報共有。
Link State Routingには2つのフェーズがあります。
Reliable Flooding
- Initial state:
- 最終状態:各ノードは隣接するノードのコストを知っている。
経路計算
各ノードは、グラフ上でダイクストラのアルゴリズムを使用して、すべてのノードへの最適経路を計算します。
- リンク状態ルーティングアルゴリズムは、あるノードからネットワーク内の他のすべてのノードへの最短経路を見つけるために使用するダイクストラのアルゴリズムとしても知られています。
- Dijkstraのアルゴリズムは反復的であり、アルゴリズムのk回目の反復の後、k個の宛先ノードに対する最小コスト経路がよく知られているという特性を持っている。 ノードiからノードjへのリンクコスト。iとjのノードが直接リンクされていない場合、c(i , j) = ∞.
- D(v).となる。 ソースコードから宛先vまでのパスのうち、現在最もコストが低いものを定義する。
- P(v):
- N:ネットワークで利用可能なノードの総数である。
アルゴリズム
InitializationN = {A} // A is a root node.for all nodes vif v adjacent to Athen D(v) = c(A,v)else D(v) = infinityloopfind w not in N such that D(w) is a minimum.Add w to NUpdate D(v) for all v adjacent to w and not in N:D(v) = min(D(v) , D(w) + c(w,v))Until all nodes in N
上記のアルゴリズムでは、初期化ステップに続いて、ループが行われる。
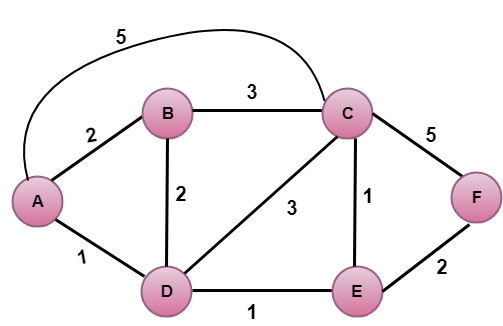
上の図で、ソース頂点はAである。
Step 1:
最初のステップは初期化ステップである。 現在知られているAから直接隣接するB、C、Dへの最小コスト経路はそれぞれ2、5、1である。 AからBへのコストは2、AからDへのコストは1、AからCへのコストは5とする。 AからEとFへのコストは、Aに直接リンクしていないため、無限大に設定されています。
| ステップ | N | D(B),P(B) | D(C),P(C) | D(D) とする。P(D) | D(E)である。P(E) | D(F)である。P(F) |
|---|---|---|---|---|---|---|
| 1 | A | 2,A | 5,A | 1,A | ∞ |
ステップ2.A.B.B.B.B.B.B.B.B.B.B.B.B.B.B:
上の表で、頂点Dはステップ1で最小コストの経路を含んでいることが分かる。
a) AからBへの最短経路の計算
b) AからCへの最短経路の計算
c) AからEへの最短経路の計算
注:頂点Dは頂点Eと直接つながっていないのでD(F)の値は無限大である。
| ステップ | N | D(B),P(B) | D(C),P(C) | D(D) となります。P(D) | D(E),P(E) | D(F),P(F) |
|---|---|---|---|---|---|---|
| 1 | A | 2,a | 5,a | 1,a | ∞ | 2 | ad | 2…φ1.5mm、φ2.5mm、φ2.5mm、φ2.5mm。A | 4,D | ∞ |
ステップ3:
上の表で、EとBの両方がステップ2で最小コストの経路を持つことが観察される。 Eの頂点を考えてみよう。 ここで、Eを通る残りの頂点の最小コスト経路を求める。
a) AからBへの最短経路を計算する。
b) AからCへの最短経路を計算する。
c) AからFへの最短経路を計算する。
| Step | N | D(B),P(B) | D(C),P(C) | D(D),P(D) | D(E),P(E) | D(F)である。P(F) |
|---|---|---|---|---|---|---|
| 1 | a | 2,a | 5,a | 1.1,a | ∞ | 2 | ad | 2,a | 4,d | 2.A | 3.A | 3.D | 3.A | 4.A | 4.A | 3.D | ∞ |
| ADE | 2,A | 3,E | 4,E |
ステップ4.D
3
∞
2,A
、E
上の表から、Bの頂点はステップ3で最もコストの低い経路を持っていることがわかります。 ここで、Bを通る残りの頂点の最短経路を求める。
a) AからCへの最短経路を計算する。
b) AからFへの最短経路を計算する。
| Step | N | D(B),P(B) | D(C),P(C) | D(D),P(D) | D(E),P(E) | D(F),P(F) | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | a | 2,a | 5,a | 1,a | ∞ | |||||||||
| ad | 2.1 | 1,a>2 | 12, | 1 | 1 | 1 | 1 | 1 | 3 | 1 | 1 | 4,d | 2,d | ∞ |
| 3 | ade | 2,a | 3,e | |||||||||||
| 4 | ADEB | 3,E | 4,E |
ステップ5:
上の表から、Cの頂点はステップ4で最もコストの低い経路を持っていることがわかります。 そこで、Cを通る残りの頂点の最小コスト経路を求める。
a) AからFへの最短経路を計算する。
| Step | N | D(B),P(B) | D(C),P(C) | D(D),P(D) | D(E),P(E) | D(F),P(F) |
|---|---|---|---|---|---|---|
| 1 | A | 2,a | 5,a | 1,a | ∞ | 2 | ad | 2,a | 4,d | 2である。d | ∞ | 3 | ade | 2,a | 3,e | 4,e | adeb | <1096>3,E | 4,E |
| 5 | ADEBC | 4,E |
最終テーブルです。
| Step | N | D(B),P(B) | D(C),P(C) | D(D)です。P(D) | D(E),P(E) | D(F),P(F) |
|---|---|---|---|---|---|---|
| 1 | a | 2,a | 5,a | 1,a | ∞ | |
| 2 | ad | 2,a | 4,d | 2,d | ∞ | |
| 3 | ade | 2.になります。a | 3,e | 4,e | ||
| 4 | adeb | 3,e | ||||
| 5 | adebc | |||||
| 6 | ADEBCF |
不利になる。
Lineステートルーティングでは、Floodingにより重いトラフィックが発生します。 Floodingは無限ループを引き起こす可能性があり、この問題はTime-to-leaveフィールド
を使用することによって解決できます。
