標準偏差とは、一連の数値がどの程度離れているかを示す数値です
標準偏差の範囲は0~無限大です。 標準偏差が0ということは、数字の羅列がすべて等しい、つまり、どの程度も離れていないことを意味します。
標準偏差 – 例
5人の応募者が就職活動の一環でIQテストを受けた。 7862> 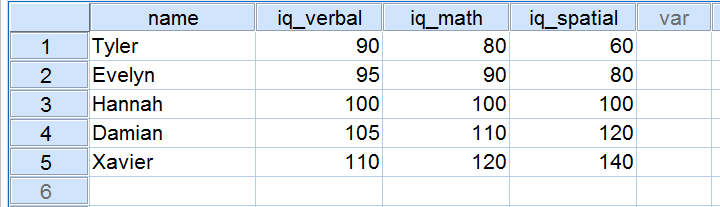
さて、3つのIQ成分の得点をよく見てみましょう。 5人の応募者の平均は、3つとも100であることに注意してください。 しかし、iq_verbalのスコアは、iq_mathのスコアよりも近くに位置しています。 さらに、iq_spatialのスコアは、最初の2つのコンポーネントのスコアよりも離れている。 いくつかのスコアがどの程度離れているかは、数字で表すことができる。
Standard Deviation – Results
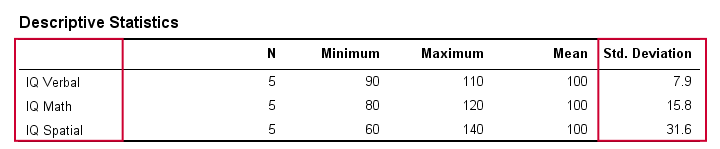
実際の生活では、生のスコアを目視して、どの程度離れているかを確認することは当然ありません。 その代わりに、いくつかのソフトウェアにそれらを計算させるだけです (詳細は後述します)。 下の表は、IQデータの標準偏差とその他の統計量を示しています。
Standard Deviation and Histogram
では、もう少し視覚的にしてみましょう。 下の図は、IQスコアの標準偏差とヒストグラムを示したものです。 各棒は、1人の応募者の1つのIQコンポーネントのスコアを表していることに注意してください。 7862> 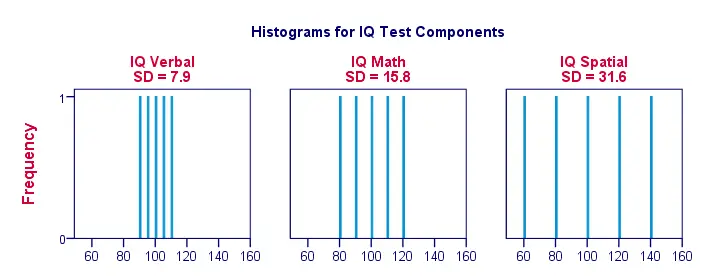
Standard Deviation – More Histograms
前の図のように、ほんの一握りの観測データを視覚化すると、簡単に明確なイメージを見ることができます。 より現実的な例として、以下に1,000個のオブザベーションのヒストグラムを紹介します。 重要なのは、これらのヒストグラムが同一の尺度を持つことです。各ヒストグラムでは、X 軸の 1 センチメートルが約 40 の「IQ 構成点」に対応します。
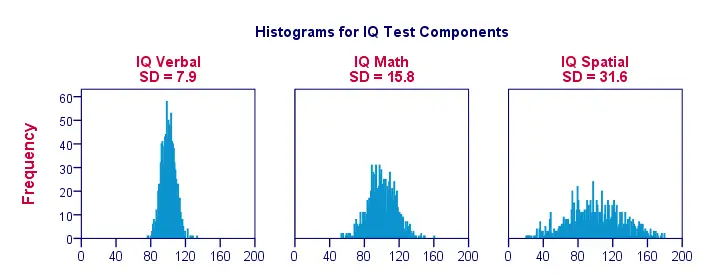
ヒストグラムによって標準偏差の概算がどのようになるかに注意してください。 より広い」ヒストグラムは、より大きな標準偏差を示し、スコア(x軸)はより離れていることを示します。 すべてのヒストグラムは同じ表面積 (1,000 件のオブザベーションに対応) を持っているので、より高い標準偏差は「より低い」ヒストグラムにも関連します。
標準偏差 – 母集団の数式
では、ソフトウェアはどのようにして標準偏差を計算しますか? さて、基本的な計算式は
$$sigma = \sqrt{Thrac{Sum(X – \mu)^2}{N}}$
where
- \(\mu) は全数の平均、
- \(\sum) は和を表します。
つまり、標準偏差は個々の数値とその平均値との差の二乗平均の平方根ということになります。
Population Formula – Software
この数式は、Google シート、OpenOffice、および Excel で、セルに =STDEVP(...) と入力することにより使用することができます。 括弧の間に標準偏差を求める数値を指定し、Enterキーを押します。
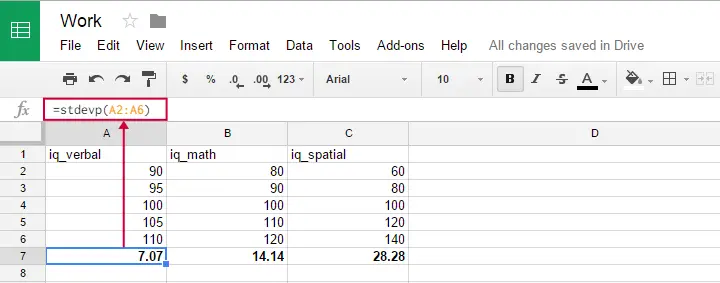
奇妙なことに、人口の標準偏差の公式は、SPSS には存在しないようです。
Standard Deviation – Sample Formula
さて、難しいことですが、あなたのデータがある(はるかに)大きな集団から単純無作為標本の場合、前の公式はこの集団の標準偏差を系統的に過小評価することになります。 S_x = \sqrt{cfrac{sum(X – \overline{X})^2}{N -1}}$
計算についてですが、最初の式と大きく違うのは \(n\) ではなく \(n -1} で割っていることです。 小さい数で割ると、結果が(少し)大きくなります。 これは、前述の過小評価を正確に補うものである。 GoogleSheets、Open Office、MS Excelでは、STDEV関数はこの2番目の数式を使用します。
標準偏差と分散
一連の数値がどの程度離れているかを表す2番目の数値が分散です。 分散は標準偏差を2乗したものです。 このことは、標準偏差と同様に、分散にも母集団と標本の式があることを意味しています。
原理的に、2つの異なる統計が基本的に数字の集合の同じ性質を表現するのは厄介なことです。 なぜ分散を捨てて標準偏差を使う(あるいはその逆)ことにしないのでしょうか。 基本的な答えは、ある状況では標準偏差がより望ましい性質を持ち、別の状況では分散がより望ましい性質を持つからです
。
