これは、アイザック・ニュートンの有名な『プリンキピア』で初めて登場した理論で、「静的」潮汐理論と呼ばれることもあります。 潮汐を発生させる力を特定した上で、ニュートンや彼に続く人々は、これらの力と静的に平衡している仮想的な地球規模の海、つまり、地球を覆う水のプロレート球体を求める平衡状態を考え出しました。 「この場合、球体は地理的な極ではなく、天体(月または太陽)に沿った極に沿って引き伸ばされ、仮想的な海の球体は変形することになる。 前のモジュールで牽引力を説明した図をもう一度見てみると、水がこれらの極に収束して双子の「潮汐の膨らみ」を作り出すことが容易に想像できます。
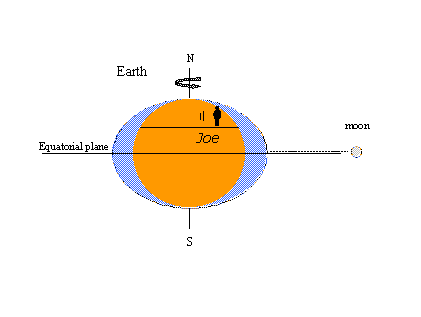
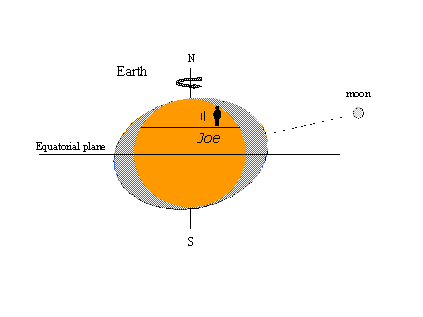
平衡理論(少なくとも潮汐の膨らみの概念)の人気の理由は、あるよく知られた潮汐現象を絵で簡単に説明できることにあります。 下の左の図は、ジョーという架空の観測者が地球と一緒に回転し、高潮という形で静的な膨らみに遭遇するもので、月がジョーの地元の子午線を横切るたびに、彼は高潮を目撃します。 12時間後に月が地球の反対側の子午線を横切ると、再び満潮になる。 時計(太陽)時間で24時間50分の1日で、2回の満潮と2回の干潮が起こる。 右の図は、月が地球の周りを公転して、赤道の北側(北偏角)に位置するようになったところです。 そのため、静止していた潮の塊が月と一直線上に移動し、日中の大潮が不同となる(高さの違う大潮が連続する)。 赤道の南北で月の傾きが最大になると、対流圏潮汐が発生する。月が赤道上にあるときに発生する潮汐を赤道潮汐と呼ぶ。対流圏-赤道潮汐は27 1/3日の間隔で2回発生し、対流圏月が月の赤経の1周期をカバーしている。 これらの観測はすべて平衡理論と一致している。
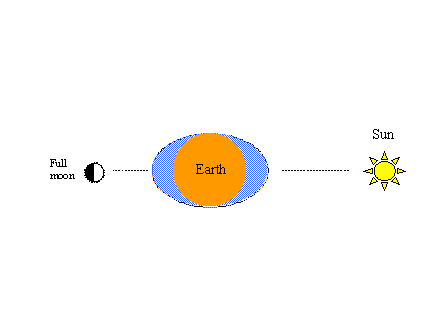
このように簡単に実証できるもう一つの現象は、よく知られている春と昼のサイクルである。 太陽の重力もまた、仮想の海に一対の潮のふくらみを作り出します。 太陽と月の牽引力が一直線に並ぶと、下左図のような大潮(高潮、低潮)となる。 3373>
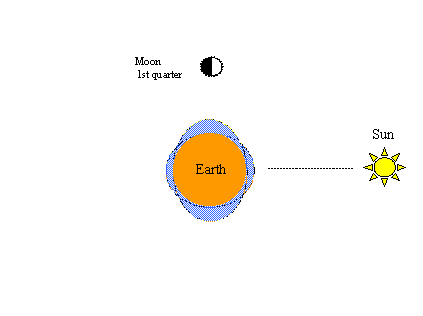
右の図は、大潮と小潮の周期のうち小潮の部分を示している。つまり、月がその周期の第1四半期(または第3四半期)にあるとき、月と太陽の牽引力は完全に一線上になく、互いに対抗する傾向があり、小潮の範囲(高さが低く、低さが高い)が生じるのである。 これは、月が太陽に対して地球を1周するのに必要な期間と同じである。
平衡理論に基づく観測潮の他の側面には、ペリジアン-アポジーン周期が含まれる。 これは、地球の周りを回る月の軌道が円ではなく楕円を描いていることに由来する。 ペリジアン潮汐は、月が地球に最も近づく近地点で発生し、アポジーン潮汐は、月が楕円軌道を描いて地球から最も遠くなる遠地点で発生します。 3373>
平衡論は周期的な潮汐現象とその多くに関連する周期を説明する優れた仕事ですが、それは理想的な行動のモデルの一例で、すべての状況で真実に忠実ではないかもしれませんが、意図した目的のために機能するものです。 そのような事例を探すのに遠くを見る必要はありません。 地球は水によって部分的にしか覆われておらず、陸地はその周りを完全に移動することを妨げ、実際の潮の動きを観察すると、理論が求めるように、月と太陽の潮を作り出す力に対して瞬時に反応しないことがわかるのです。
