投稿者:Maximilian Siebert
不均一性は恐れるべきものではなく、データに変動があることを意味するにすぎません。 ですから、異なる研究をまとめて分析したり、メタアナリシスを行ったりすれば、違いが見つかることは明らかです。 異質性の反対は均質性で、すべての研究が同じ効果を示すことを意味します
異質性には異なるタイプがあることに注意することが重要です。 参加者,介入,アウトカムにおける差異
私たちがこれらの違いに興味を持つのは、私たちの介入が毎回同じように機能していない可能性を示すことができるからです。 これらの差異を調査することで,どのような要因が介入に影響を与えるのか,また,次回に介入を実施したときにどのような結果を期待できるのか,より深く理解することができます。
臨床的・方法論的異質性は重要ですが,このブログでは統計的異質性に焦点を当てます。
異質性の特定と測定方法
アイボールテスト
フォレストプロットでは、効果推定値がどちら側にあるかよりも、信頼区間の重なりを見てください。
このことを念頭に置いて、以下のグラフを見て、どちらのプロットがより均質であるかを判断してください。 信頼区間はすべて重なっており、さらにすべての研究が対照介入を支持しています。
ただ目で見るのではなく、物事を測定するのが好きな人のために、心配しないでください、異質性の概念を理解するのに役立つ統計手法がまだいくつかあります。
カイ二乗(χ²)検定
この検定は、すべての研究が均質である、または各研究が同一の効果を測定しているという帰無仮説を仮定し、この仮説を検証するためのp値を与えてくれるものである。 この検定のp値が低ければ、仮説を棄却でき、異質性が存在することになります。
この検定は感度が低く、異質性を誤って除外してしまうことがよくあるので、多くの科学者がカットオフ値として< 0.05 でなく < 0.1 のp値を使用しています。
I²
この検定はJulian Higgins教授によって開発され、不均一性が存在するかどうかを述べるのではなく、不均一性の程度を測定する理論を持っています。
矛盾の重要性はいくつかの要因に依存するので、I2 の解釈に関する閾値は誤解を招く可能性があります。
上記の理論を理解するために、次の例を見てください。
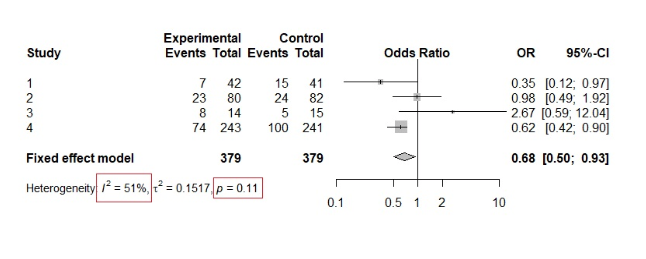
我々は、カイ2乗検定のp値が0.11で、帰無仮説を確認し、したがって同質性を示唆していることが分かります。 しかし、介入を見ることによって、我々はすでに結果にいくつかの異質性を見ることができます。 さらに、I²値は51%で、中程度から実質的な異質性を示唆しています。
これは、メタ分析にいくつかの研究しかない場合、χ2検定がいかに誤解を招くかの良い例です。
異質性に対処する方法
結果に変動があると分かったら、それを対処する必要があります。 ここでは、この問題をどのように扱うことができるかについて、いくつかの手順を紹介します。
- データに誤りがないか確認する – 入力ミスがないか戻って確認する
- 不均一性が高すぎる場合はメタアナリシスを行わない – すべてのシステマティックレビューでメタアナリシスが必要なわけではない
- 不均一性を調べる – サブグループ分析またはメタ分析によって行うことができる
- 不均一性を調べる-サブグループ分析によって行うことができる
- メタアナリシスを行わない場合はメタアナリシスを行う。regression
- ランダム効果メタアナリシスを行う – このアプローチは偶然によるもので説明できない異質性を対象とすることに留意してください
- 効果測定を変える – 例えば、リスク差を使用していて異質性が高いとします。 であれば、リスク比やオッズ比を試してみる
(1) Fletcher, J. 異質性とは何か、そしてそれは重要か? BMJ 2007; 334 :94
(3) https://www.mathsisfun.com/data/chi-square-test.html
です。
