数年前に Scott Fortmann-Roe が「バイアス-分散トレードオフの理解」と題する素晴らしいエッセーを書きました。 よりエキサイティングな側面を優先して、統計的なプロセスにあまり焦点を当てないことが多いようです (2つの例の議論はこちらとこちらをご覧ください)。
概念的な定義
これは Scott 氏のエッセイの概要であり、さらなる詳細や数学的洞察を読むことができますが、まずはこの作品の中心となっている Fortmann-Roe の逐語的定義から始めます。 もちろん、モデルは1つしかないので、予想値や平均値の話は少し変に思えるかもしれません。 しかし、モデル構築のプロセスを複数回繰り返すことができると想像してください:新しいデータを収集し、新しい分析を行い、新しいモデルを作成するたびに。 基礎となるデータセットにランダム性があるため、結果として得られるモデルは様々な予測値を持つことになります。 偏りは、これらのモデルの予測が正しい値から一般的にどれくらい外れているかを測定します。 分散による誤差:分散による誤差は、与えられたデータ点に対するモデル予測の変動としてとらえられる。 ここでも、モデル構築の全プロセスを複数回繰り返すことを想像してください。 分散は、与えられたポイントに対する予測が、モデルの異なる実現の間でどれだけ変化するかです。
本質的に、バイアスはモデルの予測が正しさからどれだけ離れているかであり、分散はこれらの予測がモデルの反復間で変化する度合いです。
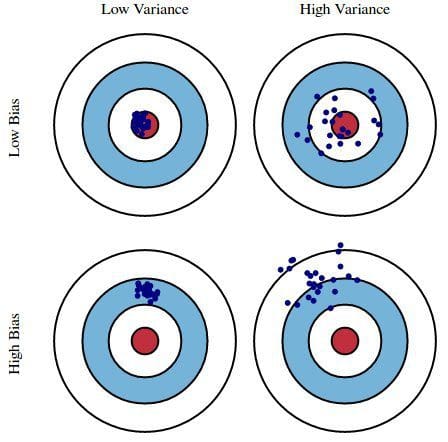
図1: バイアスと分散のグラフ図
Understanding the Bias-Variance Tradeoff, by Scott Fortmann-Roe より。
議論
単純な欠陥のある大統領選挙調査を例として、調査におけるエラーは、バイアスと分散の2つのレンズを通して説明されます:電話帳から調査参加者を選ぶことはバイアスの原因です、小さなサンプル サイズは分散の原因です。
Fortmann-Roe は次に、これらの問題を、k-Nearest Neighbor という単一のアルゴリズムに関連させて議論します。 そして、再サンプリング技術、アルゴリズムの漸近特性とバイアスおよび分散誤差への影響、データとそのモデリングの両方に対する仮定との戦いなど、バイアスと分散の管理について考えるべきいくつかの重要な問題を提供しています。 私見では、ここが最も重要なポイントです。
より多くのパラメーターがモデルに追加されると、モデルの複雑さが増し、バイアスが着実に低下する一方で分散が主要な関心事となります。 たとえば、線形回帰に多くの多項式項が追加されるほど、結果として得られるモデルの複雑さは大きくなります。 言い換えれば、バイアスはモデルの複雑さに反応して負の一階微分を持ち、分散は正の傾きを持ちます。

Fig. 2: バイアスと分散が全体の誤差に貢献
Understanding the Bias-Variance Tradeoff, by Scott Fortmann-Roe より引用。
Fortmann-Roe は、過剰適合と過小適合に関するセクションの最後に、彼の素晴らしいエッセイ (Accurately Measuring Model Prediction Error) を紹介し、「クロスバリデーションなどのリサンプリングに基づく測定は、Aikake の情報基準などの理論的測定よりも好まれるべきである」という非常に同意できる推奨に移っています。
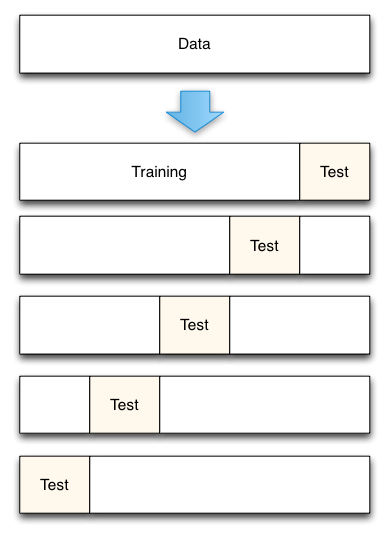
Fig. 3: 5-Fold cross-validation data split
From Accurately Measuring Model Prediction Error, by Scott Fortmann-Roe.より。
もちろん、クロスバリデーションでは、使用するフォルド数 (k-fold cross-validation ですね)、k の値が重要な決定となります。 値が小さいほど、誤差推定の偏りが大きくなり、分散が小さくなります。 逆に、kをインスタンス数と同じにすると、そのときの誤差推定値はバイアスは非常に小さくなりますが、分散が大きくなる可能性があります。 9273>
残念ながら、クロスバリデーションも、データサイエンスの現代ではその魅力を失っているように思えることがありますが、それはまた別の機会にお話しします。
Scott Fortmann-Roe 氏のバイアス-分散トレードオフに関するエッセイ全体と、モデル予測誤差の測定に関する彼の記事を読むことをお勧めします。 レビュー
