Download: Prioritization Matrix Template (XLS)
優先順位付けマトリックスとは?
優先順位付けマトリックスの構築方法
優先順位付けマトリックスの例
その他の情報
ソース
Prioritization Matrixとは何でしょうか?
優先順位付けマトリックスは、基準の選択、重み付け、および適用を通じて選択肢を体系的に比較することによって選択肢を絞り込み、組織が意思決定を行うのを支援することができます。 優先順位付けマトリックス
- 基本的な意見の相違を素早く表面化させ、意見の相違をオープンに解決できる
- チームに、すべての解決策から最適な解決策に絞り込むように強制する。
- 選択肢の最前面に意思決定基準をもたらすことによって、「隠れた意図」を制限する
- プロセスの各ステップの後に合意を求めることによって、フォロースルーを増やす
優先順位付けマトリックスの構築方法
優先順位付けマトリックスの構築方法は、3通りある。 が、以下は完全分析基準法について詳しく説明します。 この具体的な方法は、少数の選択肢(5~10個の選択肢)と少数の基準(3~6個の基準)を必要とする小グループ(3~8人)で使うのが最適である。 また、この具体的な方法では、クライテリアとオプションについてチームが完全なコンセンサスに達する必要がある。 計画が失敗した場合の賭け金は高くなる可能性がある。
目標を設定する
最終的な目標に合意するために、グループは合意によって明確な目標声明を作成する必要がある。
![]()
基準を設定する
利用可能な文書やガイドラインを調べて、基準のリストを作成する。 チームは基準とその意味についてコンセンサスを得なければならず、そうでなければプロセスは失敗する可能性が高い。

3.基準の重要性を評価する
どの基準が最も重要かを決めるために、マトリックスを使ってそれぞれの基準を別の基準に対して重み付けする
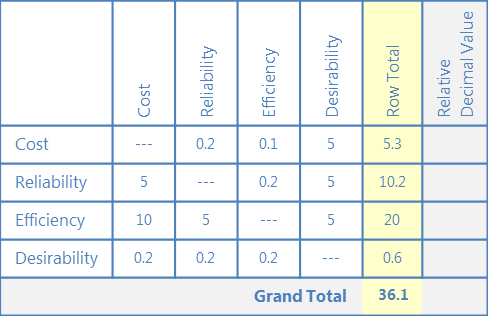
A. 基準を書く
列の一番上に基準を書く。 最後に「行の合計」と「相対的な小数値」の列を追加します (これらは後で使用します)。 各行の最初に条件を書きます。
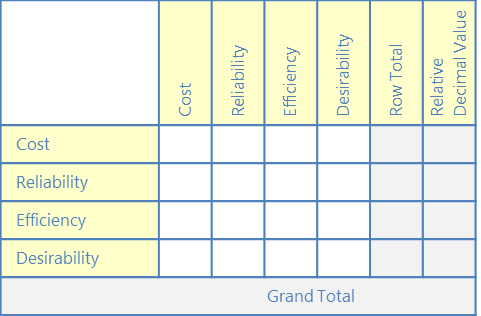
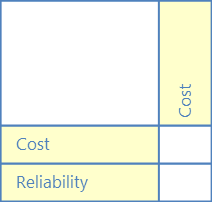
B. 基準の重み付け
どの基準がより重要であるかを決定するプロセスを開始します。 (基準をそれ自身と比較することはできないので、最初の列の 2 番目のセルから開始します)。
このセルで、左側の基準(信頼性)が上の基準(コスト)よりも重要かどうか自問してください。 より重要かどうか、またどの程度重要かを示すために、次の重み付けシステムを使用してください。
10 = 非常に重要
5 = より重要
1 = 同じくらい重要
0.2 = あまり重要ではない
0.1 = かなり重要ではない
注:整数(10、5、1)は常に「望ましい」評価を表すものとします。 ある場合は、何かの「多さ」(例:重要性、信頼性、教育的価値)を意味し、ある場合は「少なさ」(例:コスト、移動時間)を意味します。
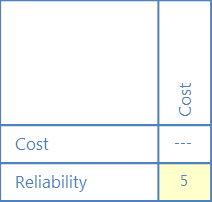 |
これはコストより信頼性が重要(5)であることを表しています。 |
行セルに重みを記録するたびに、対応する列セルにその逆数を記録する必要があります。
Weight of 10 –>Reciprocal value of 0.1
Weight of 5 –>Reciprocal value of 0.2
Weight of 1 –>Reciprocal value of 1
Weight of 0.2 –>Reciprocal value of 5
Weight of 0.2–
Weight of 5
Reciprocal value of 0.2– Weight of 10 — Reciprocal value of 1
Weight of 1
Reciprocal value of 0.21 –>Reciprocal value of 10
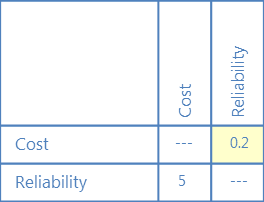 |
5の逆数値は0.2であり、これはコストが信頼性よりも重要でない(0.2)ことを示している。 |
残りの基準にも引き続き重みを付け、逆数を記録する。
C. 合計を計算する
終了したら、各横列を合計し、”Row Total “に合計を入力します。 すべての行の合計を足して、総計を算出します。
D. 基準加重を計算する
各行の合計を総計で割り、”相対的な小数値” にこれを入力します。
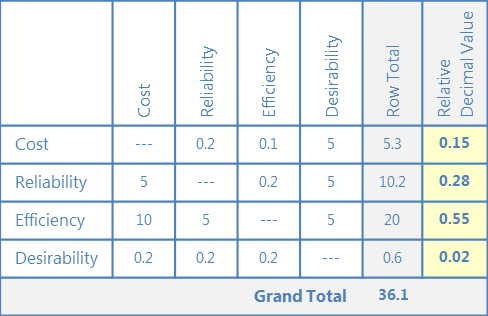
これらの相対的な小数値は、各基準があなたにとってどれだけ相対的に重要かを示しています-これらは現在、あなたの “基準加重” と呼ばれています。
基準の重み付けは、プロセスの最後、ステップ6で選択肢を比較するために使用します。 基準に対する選択肢の重み付け
どの選択肢が基準を最もよく満たすかを決定し始めるために、与えられた基準内で選択肢を重み付けするためにマトリックスのセットを使用します。
A. 選択肢の重み付け
上記と同じ重み付けと方法を使用して、1つの基準をそれ自身のマトリックスの左上隅に配置し、選択肢を互いに重み付けします。 重みを使用して、どの選択肢がマトリックスの1つの基準をよりよく満たすかを示します。
覚えておいてください。 整数 (10、5、1) は常に「望ましい」評価を表す必要があります。 あるケースでは、これは何かの「より多くの」(例:重要性、信頼性、教育的価値)を意味し、他のケースでは「より少ない」(例:コスト、移動時間)を意味することがあります。
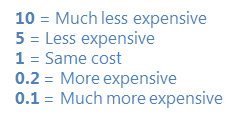
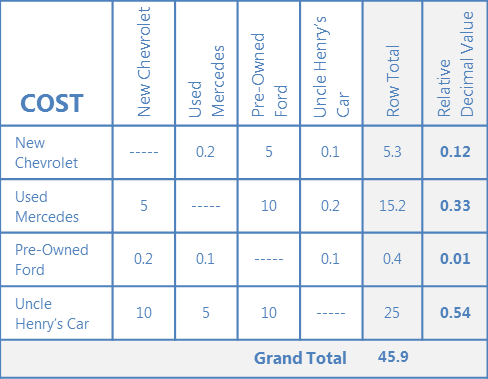
各基準(コスト、信頼性、効率、望ましさ)について、同じ選択肢と重み付け方法で、各基準の行列ができるまでこのステップを繰り返します。 基準の数だけマトリクスが存在することになります。
これらの相対的な10進値は、各オプションが与えられた基準をどの程度満たしているかを示しています。
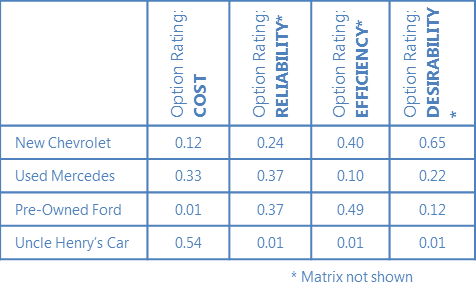
B. オプションです。 選択肢の評価をまとめる
混乱を最小限に抑えるために、各マトリックスから選択肢の評価を1つの表にまとめると便利です。
オプションを比較する
別のL型マトリックスを使用して、すべての組み合わせられた基準に基づいて、各オプションを比較します。
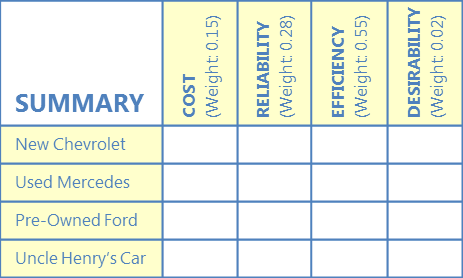
A. サマリーマトリックスを作成する
各列の一番上に、ステップ3で設定したそれぞれの基準の重み付け値とともに、基準をリストアップします。 各選択肢を行の最初に書きます。
B. 基準重み付けと選択肢の評価を掛け合わせる
各セルで、基準重み付け値(各列の一番上にある)を、ステップ4の各マトリクスからの選択肢の評価と掛け合わせる。
 |
ステップ4のコストマトリックスからの新車シボレーオプション評価 = 0.12 ステップ4のコストマトリックスからの中古メルセデスオプション評価 = 0.33 ステップ4のコストマトリックスからの中古フォードオプション評価 = 0.0.01 Uncle Henry’s Car オプション評価(ステップ 4 のコスト行列より) = 0.54 |


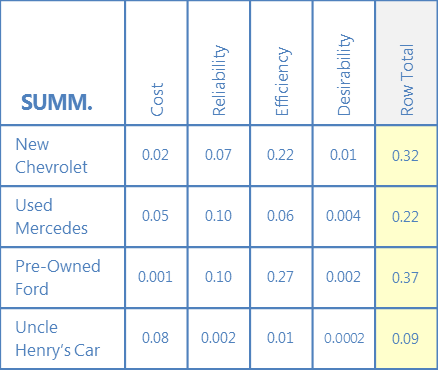
これをオプションと基準ごとに繰り返し、ステップ 3 と 4 から値を取得します。 行の合計を計算する
行の合計に到達するために、各行にわたって値を追加します。
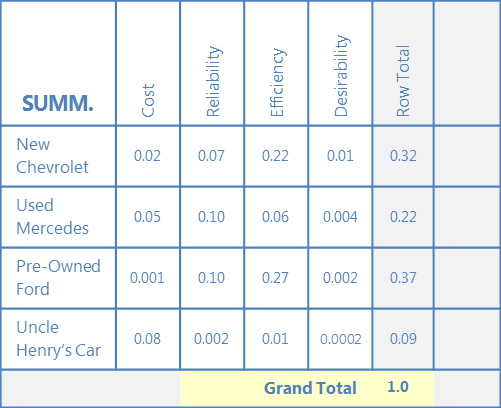
D. グランドトータルを計算
グランドトータルに到達するために、すべての行の合計を追加します。
E. 相対小計を計算する
各行の合計を総計で割り、これを “相対小計 “に入力します。
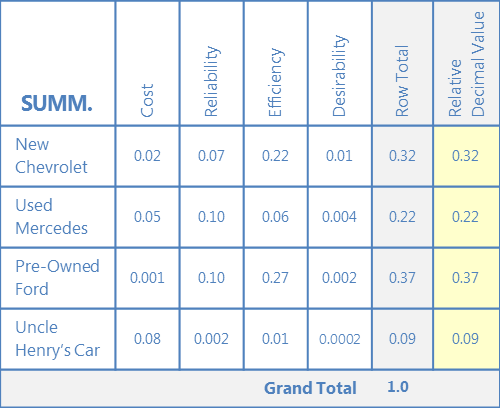
6.すべての基準で最良の選択肢を選ぶ
相対的小数値を比較して、どの選択肢が最も高いかを決定します。 これは、オプションと基準が与えられた最良の選択です。

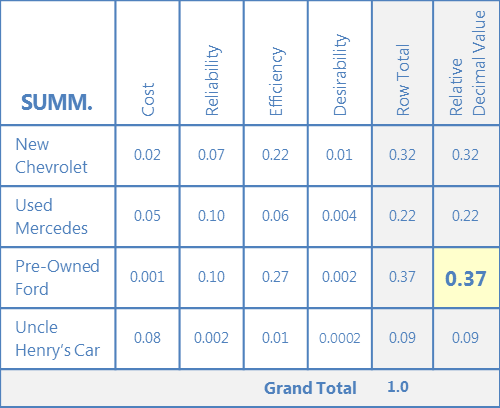
優先順位付けマトリックスの例
おいしいポップコーンを調理する。 古いQIツールを新しい方法で使う
全米郡市保健担当者協会(NACCHO)
戦略優先順位付けマトリクス(DOC)
ヘルシーカンザス2010
