För några år sedan skrev Scott Fortmann-Roe en bra uppsats med titeln ”Understanding the Bias-Variance Tradeoff”.
Som datavetenskap förvandlas till ett accepterat yrke med en egen uppsättning av verktyg, förfaranden, arbetsflöden, etc., verkar det ofta finnas mindre fokus på statistiska processer till förmån för de mer spännande aspekterna (se här och här för ett par exempel på diskussioner).
Begreppsdefinitioner
Medans detta kommer att fungera som en översikt över Scotts uppsats, som du kan läsa för ytterligare detaljer och matematiska insikter, kommer vi att börja med Fortmann-Roe’s ordagranna definitioner som är centrala för stycket:
Fel på grund av bias: Felet på grund av bias tas som skillnaden mellan vår modells förväntade (eller genomsnittliga) förutsägelse och det korrekta värde som vi försöker förutsäga. Naturligtvis har du bara en modell så att tala om förväntade eller genomsnittliga prediktionsvärden kan verka lite konstigt. Tänk dig dock att du skulle kunna upprepa hela modellbyggnadsprocessen mer än en gång: varje gång du samlar in nya data och genomför en ny analys skapar du en ny modell. På grund av slumpmässigheten i de underliggande datamängderna kommer de resulterande modellerna att ha en rad olika förutsägelser. Bias mäter hur långt dessa modellers förutsägelser generellt sett avviker från det korrekta värdet.
Fel på grund av varians: Felet på grund av varians är variabiliteten hos en modellförutsägelse för en given datapunkt. Återigen, tänk dig att du kan upprepa hela modellbyggnadsprocessen flera gånger. Variansen är hur mycket förutsägelserna för en given punkt varierar mellan olika realiseringar av modellen.
I huvudsak är bias hur långt ifrån korrekt en modells förutsägelser är, medan variansen är i vilken grad dessa förutsägelser varierar mellan modellens iterationer.
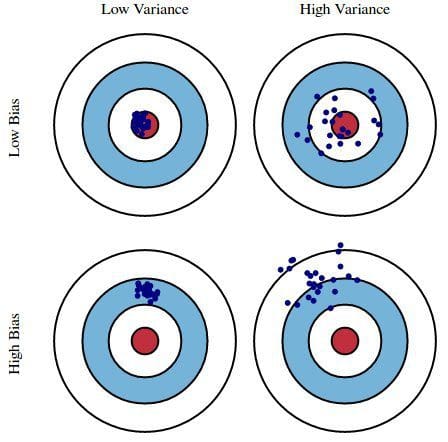
Figur 1: Grafisk illustration av bias och varians
Från Understanding the Bias-Variance Tradeoff, av Scott Fortmann-Roe.
Diskussion
Med en enkel, bristfällig undersökning av presidentvalet som exempel förklaras sedan felen i undersökningen med hjälp av de dubbla linserna bias och varians: att välja undersökningsdeltagare från en telefonbok är en källa till bias; en liten urvalsstorlek är en källa till varians; att minimera det totala modellfelet är beroende av en balansering av bias- och variansfel.
Fortmann-Roe fortsätter sedan att diskutera dessa frågor i samband med en enda algoritm: k-Nearest Neighbor. Han ger sedan några nyckelfrågor att tänka på när man hanterar bias och varians, bland annat omprovtagningstekniker, asymptotiska egenskaper hos algoritmer och deras effekt på bias- och variansfel, och att bekämpa sina antaganden både när det gäller data och dess modellering.
Den avslutar uppsatsen med att hävda att dessa två begrepp i grund och botten är tätt sammankopplade med både över- och underanpassning. Enligt min mening är här den viktigaste punkten:
När fler och fler parametrar läggs till i en modell ökar modellens komplexitet och variansen blir vårt främsta bekymmer medan bias stadigt sjunker. Till exempel, ju fler polynomiala termer som läggs till i en linjär regression, desto större blir den resulterande modellens komplexitet. Med andra ord har bias en negativ första ordningens derivat som svar på modellens komplexitet medan variansen har en positiv lutning.

Fig. 2: Bias och varians bidrar till det totala felet
Från Understanding the Bias-Variance Tradeoff, av Scott Fortmann-Roe.
Fortmann-Roe avslutar avsnittet om över- och underanpassning med att peka på en annan av sina utmärkta uppsatser (Accurately Measuring Model Prediction Error), och går sedan vidare till den mycket instämmande rekommendationen att ”resamplingbaserade åtgärder som korsvalidering bör föredras framför teoretiska åtgärder som Aikakes informationskriterier”.
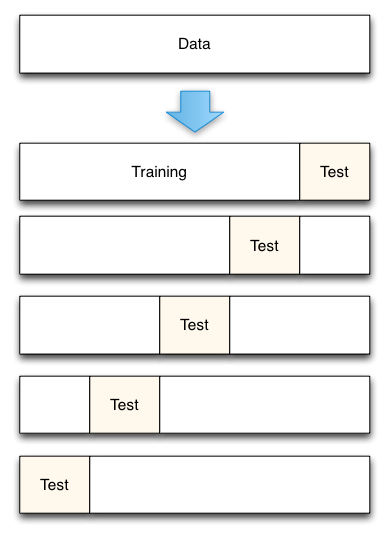
Fig. 3: 5-Fold cross-validation data split
Från Accurately Measuring Model Prediction Error, av Scott Fortmann-Roe.
När det gäller korsvalidering är naturligtvis antalet folds som ska användas (k-fold cross-validation, eller hur?), värdet på k ett viktigt beslut. Ju lägre värde, desto högre bias i feluppskattningarna och desto mindre varians. Omvänt, när k sätts lika med antalet instanser, är felskattningen då mycket låg i bias men har möjlighet till hög varians. Det är uppenbart att det är viktigt att förstå kompromissen mellan bias och varians även för de mest rutinmässiga statistiska utvärderingsmetoderna, t.ex. k-fold korsvalidering.
Tyvärr tycks korsvalidering ibland ha förlorat sin attraktionskraft i datavetenskapens moderna tidsålder, men det är en diskussion som kan tas upp vid ett annat tillfälle.
Jag rekommenderar att du läser Scott Fortmann-Roes hela uppsats om bias-varians tradeoff, liksom hans stycke om att mäta modellens prediktionsfel.
Relaterat:
- Big Data, Bible Codes, and Bonferroni
- Datavetenskap om variabelval: En översyn
- Databaser över algoritmer
