Link State Routing är en teknik där varje router delar kunskapen om sitt grannskap med alla andra routrar i internetnätverket.
De tre nycklarna för att förstå Link State Routing-algoritmen:
- Kunskap om grannskapet: Istället för att skicka sin routningstabell skickar en router endast information om sitt grannskap. En router sänder sina identiteter och kostnader för de direktanslutna länkarna till andra routrar.
- Flooding: Varje router skickar informationen till alla andra routrar i internetnätverket utom sina grannar. Denna process kallas Flooding (översvämning). Varje router som tar emot paketet skickar kopiorna till alla sina grannar. Slutligen får varje enskild router en kopia av samma information.
- Informationsdelning: En router skickar informationen till varje annan router endast när det sker en förändring i informationen.
Link State Routing har två faser:
Reliable Flooding
- Initialt tillstånd: Varje nod känner till kostnaderna för sina grannar.
- Slutligt tillstånd: Varje nod känner till hela grafen.
Ruttberäkning
Varje nod använder Dijkstras algoritm på grafen för att beräkna de optimala vägarna till alla noder.
- Link state routing-algoritmen är också känd som Dijkstras algoritm som används för att hitta den kortaste vägen från en nod till alla andra noder i nätverket.
- Dijkstras algoritm är iterativ och har egenskapen att efter den k:e iterationen av algoritmen är de minst kostsamma vägarna välkända för k destinationsnoder.
Låt oss beskriva några notationer:
- c( i , j): Om noderna i och j inte är direkt länkade är c(i , j) = ∞.
- D(v): Det definierar kostnaden för den väg från källkod till destination v som för närvarande har den lägsta kostnaden.
- P(v): Den definierar kostnaden för den väg från källkod till destination v som för närvarande har den lägsta kostnaden: Den definierar den föregående noden (granne till v) tillsammans med den aktuella vägen med lägst kostnad från källkod till v.
- N: Det är det totala antalet noder som finns tillgängliga i nätverket.
Algoritm
InitializationN = {A} // A is a root node.for all nodes vif v adjacent to Athen D(v) = c(A,v)else D(v) = infinityloopfind w not in N such that D(w) is a minimum.Add w to NUpdate D(v) for all v adjacent to w and not in N:D(v) = min(D(v) , D(w) + c(w,v))Until all nodes in N
I ovanstående algoritm följs ett initialiseringssteg av en slinga. Antalet gånger som slingan utförs är lika med det totala antalet noder som finns i nätverket.
Låt oss förstå genom ett exempel:
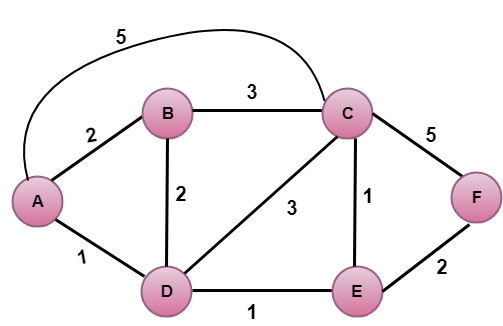
I figuren ovan är källvertexet A.
Steg 1:
Det första steget är ett initialiseringssteg. Den för närvarande kända minsta kostnadsvägen från A till dess direkt anslutna grannar B, C och D är 2, 5 respektive 1. Kostnaden från A till B sätts till 2, från A till D sätts till 1 och från A till C sätts till 5. Kostnaden från A till E och F sätts till oändligt eftersom de inte är direkt kopplade till A.
| Steg | N | D(B),P(B) | D(C),P(C) | D(D),P(D) | D(E),P(E) | D(F),P(F) |
|---|---|---|---|---|---|---|
| 1 | A | 2,A | 5,A | 1,A | ∞ | ∞ |
Steg 2:
I tabellen ovan ser vi att vertex D innehåller den minst kostsamma vägen i steg 1. Därför läggs den till i N. Nu måste vi bestämma en väg med minsta kostnad genom vertex D.
a) Beräkning av kortaste vägen från A till B
b) Beräkning av kortaste vägen från A till C
c) Beräkning av kortaste vägen från A till E
Notera: Vertex D har ingen direkt koppling till vertex E. Därför är värdet på D(F) oändligt.
| Steg | N | D(B),P(B) | D(C),P(C) | D(D),P(D) | D(E),P(E) | D(F),P(F) |
|---|---|---|---|---|---|---|
| 1 | A | 2,A | 5,A | 1,A | ∞ | ∞ |
| 2 | AD | 2,A | 4,D | 2,D | ∞ |
Steg 3:
I tabellen ovan ser vi att både E och B har den minst kostsamma vägen i steg 2. Låt oss betrakta E:s topp. Nu bestämmer vi den minst kostsamma vägen för resterande hörn genom E.
a) Beräkna den kortaste vägen från A till B.
b) Beräkna den kortaste vägen från A till C.
c) Beräkna den kortaste vägen från A till F.
| Steg | N | D(B),P(B) | D(C),P(C) | D(D),P(D) | D(E),P(E) | D(F),P(F) | |
|---|---|---|---|---|---|---|---|
| 1 | A | 2,A | 5,A | 1,A | ∞ | ∞ | |
| 2 | AD | 2,A | 4,D | 2,D | ∞ | ||
| 3 | ADE | 2,A | 3,E | 4,E |
Steg 4:
I tabellen ovan ser vi att B-höjden har den minst kostsamma vägen i steg 3. Därför läggs den till i N. Nu bestämmer vi den minst kostsamma vägen för de återstående topparna genom B.
a) Beräkning av den kortaste vägen från A till C.
b) Beräkning av den kortaste vägen från A till F.
| Steg | N | D(B),P(B) | D(C),P(C) | D(D),P(D) | D(E),P(E) | D(F),P(F) | |
|---|---|---|---|---|---|---|---|
| 1 | A | 2,A | 5,A | 1,A | ∞ | ∞ | |
| 2 | AD | 2,A | 4,D | 2,D | ∞ | ||
| 3 | ADE | 2,A | 3,E | 4,E | |||
| 4 | ADEB | 3,E | 4,E |
Steg 5:
I tabellen ovan ser vi att C vertex har den minst kostsamma vägen i steg 4. Därför läggs den till i N. Nu bestämmer vi den minst kostsamma vägen för de återstående topparna genom C.
a) Beräkning av den kortaste vägen från A till F.
| Steg | N | D(B),P(B) | D(C),P(C) | D(D),P(D) | D(E),P(E) | D(F),P(F) | ||
|---|---|---|---|---|---|---|---|---|
| 1 | A | 2,A | 5,A | 1,A | ∞ | ∞ | ||
| 2 | AD | 2,A | 4,D | 2,D | ∞ | |||
| 3 | ADE | 2,A | 3,E | 4,E | ||||
| 4 | ADEB | 3,E | 4,E | |||||
| 5 | ADEBC | 4,E |
Slutlig tabell:
| Steg | N | D(B),P(B) | D(C),P(C) | D(D),P(D) | D(E),P(E) | D(F),P(F) | ||
|---|---|---|---|---|---|---|---|---|
| 1 | A | 2,A | 5,A | 1,A | ∞ | ∞ | ||
| 2 | AD | 2,A | 4,D | 2,D | ∞ | |||
| 3 | ADE | 2,A | 3,E | 4,E | ||||
| 4 | ADEB | 3,E | 4,E | |||||
| 5 | ADEBC | 4,E | ||||||
| 6 | ADEBCF |
Nedsättning:
Den tunga trafiken skapas i Line state routing på grund av översvämning. Flooding kan orsaka en oändlig looping, detta problem kan lösas genom att använda Time-to-leave-fältet
.
