Aplicação do teorema de Buckingham Pi

Próximo: Importância dos números não-dimensionais para cima: Teorema de Buckingham Pi Anterior: Teorema de Buckingham Pi

Aplicação do teorema de Buckingham Pi

O teorema que temos dito é muito geral, mas não limitado à Mecânica dos Fluidos. É usado em campos diversificados como Botânica e Ciências Sociais e foram escritos livros e volumes sobre este tema. Mas não precisamos de muita teoria para poder aplicá-lo. O que vamos considerar é um procedimento para usar o teorema e chegar a números não dimensionais para um determinado fluxo.

1. Listar todas as variáveis que governam o processo. Estas variáveis devem ser independentes umas das outras. Por exemplo, não se deve escolher densidade, gravidade e peso específico. Densidade e Peso Específico devem servir. Para o nosso problema temos F, D, V, e . Temos n = 5,
2. Marcar as variáveis de repetição. No nosso caso estas são D, V e fazendo k = 3 .
3. Decidir quantos números não-dimensionais existem. Para o nosso caso, temos n – k = 2. Nosso problema tem 2 números não-dimensionais, e .
4. Definir os números não-dimensionais agrupando as variáveis em n – k grupos para que cada grupo tenha todas as variáveis repetitivas e uma variável não repetitiva. Assim para o nosso problema temos

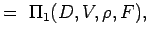
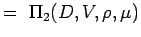
   >		(5.2)
   Let
   >
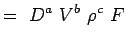
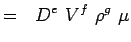   >	>	(5.3)

5. Expresse agora cada variável em termos das suas dimensões. Vamos usar o sistema MLT de acordo com o qual as variáveis para os nossos problemas têm as seguintes dimensões.
   

   >Variável	Dimensões
   F, Força	M L / T2 ou M L T-2
   D, Diâmetro:	L
   V, Velocidade	L/T ou LT-1
   , Densidade:	M/L3 ou ML-3
   , Viscosidade	ML-1T-1

   Substituindo estas dimensões em Eqn. 5.2, temos

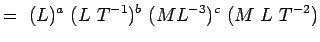
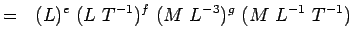
   		(5.4)
   Or
   >
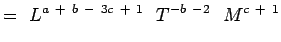
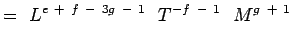
   		(5.5)

   Notando que e são não-dimensionais que temos,

   a + b – 3c + 1 = 0; -b – 2 = 0, c + 1 = 0
   e + f – 3g – 1 = 0; -f – 1 = 0;g + 1 = 0	(5.6)

   Solucionando os rendimentos das equações,

   a = -2, b = -2, c = -1
   e = -1, f = -1, g = -1	(5.7)

   Agora os nossos números não-dimensionais tornam-se,

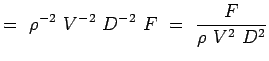
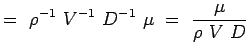
   >		(5.8)

Assim encontramos os números não-dimensionais para o fluxo de interesse, ou seja, o arrastamento em torno de um cilindro circular. A relação funcional entre os dois números pode ser expressa como

Mas note que a forma do termo que derivamos é um pouco diferente do que assumimos no início. O lado direito da equação é na verdade o inverso do número de Reynolds! Isto aponta para a desvantagem da análise de que a forma exata entre os números não pode ser obtida. Qualquer coeficiente ou índice obtido não pode ser determinado por esta análise. Isto deve ser determinado pela experimentação ou por bycomputações. Mas como os números são não-dimensionais nós escrevemos canalways,

Next: Importância dos números não-dimensionais para cima: Teorema de Buckingham Pi Anterior: Teorema de Buckingham Pi

(c) Aeroespacial, Mecânico & Eng. Mecatrônico. 2005
Universidade de Sydney