Um desvio padrão é um número que nos diz
até que ponto um conjunto de números se separa. Um desvio padrão pode variar de 0 a infinito. Um desvio padrão de 0 significa que uma lista de números são todos iguais – eles não se separam de forma alguma.
Desvio padrão – Exemplo
Cinco candidatos fizeram um teste de QI como parte de uma candidatura a um emprego. As suas notas em três componentes de QI são mostradas abaixo.
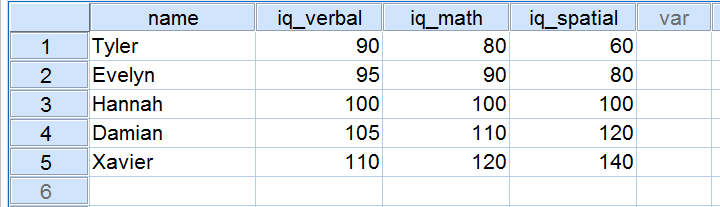
Agora, vamos ver de perto as notas nos 3 componentes de QI. Note que todos os três têm uma média de 100 sobre os nossos 5 candidatos. Contudo, as pontuações no iq_verbal estão mais próximas umas das outras do que as pontuações no iq_math. Além disso, as notas no iq_spatial estão mais afastadas do que as notas nos dois primeiros componentes. A medida exacta em que uma série de pontuações se encontram separadas pode ser expressa como um número. Este número é conhecido como desvio padrão.
Desvio padrão – Resultados
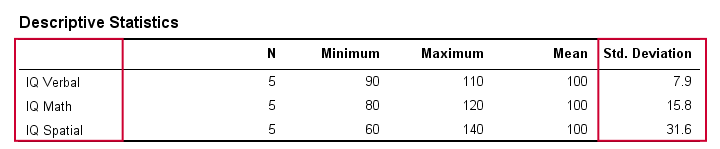
Na vida real, obviamente não inspecionamos visualmente as pontuações brutas para ver até que ponto elas se afastam. Em vez disso, nós simplesmente teremos algum software para calculá-las para nós (mais sobre isso mais tarde). A tabela abaixo mostra os desvios padrão e algumas outras estatísticas para os nossos dados de QI. Note que os desvios padrão confirmam o padrão que vimos nos dados brutos.
Desvio Padrão e Histograma
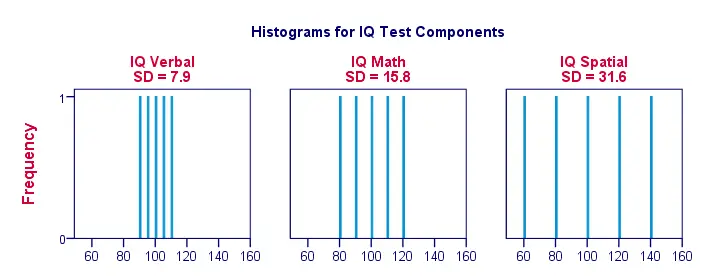
Direito, vamos tornar as coisas um pouco mais visuais. A figura abaixo mostra os desvios padrão e os histogramas para as nossas pontuações de QI. Note que cada barra representa a pontuação de 1 candidato em 1 componente de QI. Mais uma vez, vemos que os desvios padrão indicam até que ponto as pontuações estão separadas.
Desvio Padrão – Mais Histogramas
Quando visualizamos dados em apenas um punhado de observações como na figura anterior, facilmente vemos uma imagem clara. Para um exemplo mais realista, vamos apresentar abaixo histogramas para 1.000 observações. É importante notar que estes histogramas têm escalas idênticas; para cada histograma, um centímetro no eixo x corresponde a cerca de 40 ‘pontos de componente de QI’.
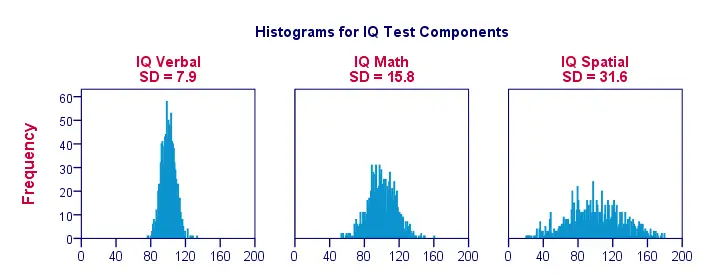
Notem como os histogramas permitem estimativas aproximadas de desvios padrão. Os histogramas ‘Wider’ indicam desvios padrão maiores; as pontuações (eixo x) estão mais afastadas. Como todos os histogramas têm áreas de superfície idênticas (correspondentes a 1.000 observações), desvios padrão mais altos também estão associados a histogramas ‘inferiores’.
Desvio Padrão – Fórmula Populacional
Então, como o seu software calcula os desvios padrão? Bem, a fórmula básica é
$$\sigma = \sqrt{\frac{\sum(X – \mu)^2}{N}}$$
where
- \(X\) denota cada número separado;
- (\u) denota a média sobre todos os números e
- (\sum) denota uma soma.
Em palavras, o desvio padrão é a raiz quadrada da diferença quadrática média entre cada número individual e a média destes números.
Importante, esta fórmula assume que os seus dados contêm toda a população de interesse (daí a “fórmula da população”). Se os seus dados contêm apenas uma amostra da sua população alvo, veja abaixo.
Population Formula – Software
Você pode usar esta fórmula em planilhas do Google, OpenOffice e Excel digitando =STDEVP(...) em uma célula. Especifique os números sobre os quais você quer o desvio padrão entre os parênteses e pressione Enter. A figura abaixo ilustra a idéia.
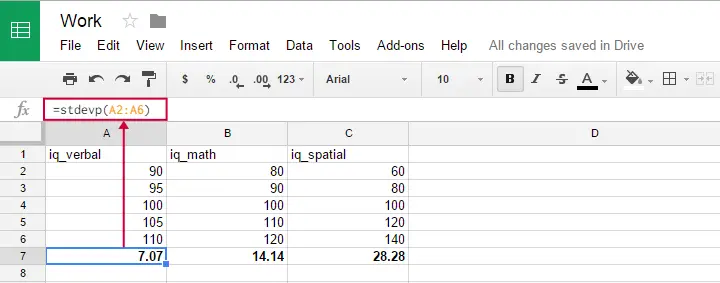
Formula de desvio padrão da população não parece existir no SPSS.
Desvio Padrão – Fórmula Amostra
Agora para algo desafiador: se seus dados são (aproximadamente) uma simples amostra aleatória de alguma (muito) população maior, então a fórmula anterior irá sistematicamente subestimar o desvio padrão nesta população. Um estimador imparcial para o desvio padrão da população é obtido usando-se
$$S_x = \sqrt{\frac{\sum(X – \sum sobrelinha{X})^2}{N -1}}$$
Cálculos, a grande diferença com a primeira fórmula é que dividimos por \s(n -1) em vez de \s(n). Dividir por um número menor resulta em um resultado (ligeiramente) maior. Isto compensa precisamente a subestimação acima mencionada. Para amostras grandes, porém, as duas fórmulas têm resultados praticamente idênticos.
No GoogleSheets, Open Office e MS Excel, a função STDEV utiliza esta segunda fórmula. É também a (única) fórmula de desvio padrão implementada em SPSS.
Desvio Padrão e Desvio
Um segundo número que expressa até que ponto um conjunto de números está separado é a variância. A variância é o desvio padrão ao quadrado. Isto implica que, similar ao desvio padrão, a variância tem uma população assim como uma fórmula de amostra.
Em princípio, é estranho que duas estatísticas diferentes expressem basicamente a mesma propriedade de um conjunto de números. Por que não descartamos a variância em favor do desvio padrão (ou inversamente)? A resposta básica é que o desvio padrão tem propriedades mais desejáveis em algumas situações e a variância em outras.
