A poucos anos atrás, Scott Fortmann-Roe escreveu um grande ensaio intitulado “Understanding the Bias-Variance Tradeoff”
As data science morphs into an accepted profession with its own set of tools, procedures, workflows, etc, muitas vezes parece haver menos foco nos processos estatísticos em favor dos aspectos mais excitantes (veja aqui e aqui para um par de exemplos de discussões).
Conceitual Definitions
Embora isso sirva como uma visão geral do ensaio de Scott, que você pode ler para mais detalhes e insights matemáticos, começaremos com as definições verbais de Fortmann-Roe que são centrais para a peça:
Error due to Bias: O erro devido a bias é tomado como a diferença entre a previsão esperada (ou média) do nosso modelo e o valor correto que estamos tentando prever. É claro que você tem apenas um modelo, então falar sobre valores de previsão esperados ou médios pode parecer um pouco estranho. No entanto, imagine que você poderia repetir todo o processo de construção do modelo mais de uma vez: cada vez que você reunir novos dados e executar uma nova análise criando um novo modelo. Devido à aleatoriedade nos conjuntos de dados subjacentes, os modelos resultantes terão uma gama de previsões. O viés mede quão longe em geral as previsões desses modelos estão do valor correto.
Error devido ao Desvio: O erro devido ao desvio é tomado como a variabilidade da previsão de um modelo para um determinado ponto de dados. Novamente, imagine que você pode repetir o processo inteiro de construção do modelo várias vezes. A variância é o quanto as previsões para um dado ponto variam entre diferentes realizações do modelo.
Essencialmente, o viés é como as previsões de um modelo são removidas da exatidão, enquanto a variância é o grau em que essas previsões variam entre as iterações do modelo.
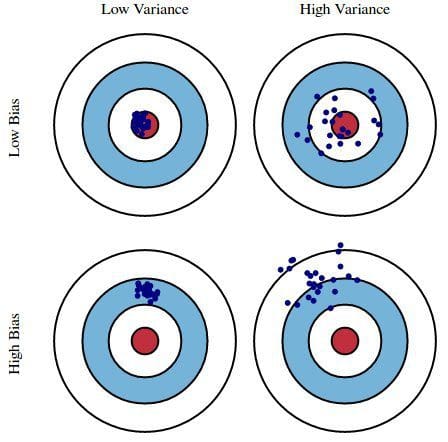
Fig. 1: Ilustração gráfica do viés e da variância
De acordo com o Bias-Variance Tradeoff, de Scott Fortmann-Roe.
Discussão
Usando como exemplo uma simples sondagem eleitoral presidencial com falhas, os erros na sondagem são então explicados através das lentes gêmeas de viés e variância: a seleção dos participantes da sondagem a partir de uma lista telefônica é uma fonte de viés; um pequeno tamanho de amostra é uma fonte de variância; a minimização do erro total do modelo depende do equilíbrio dos erros de viés e variância.
Fortmann-Roe, em seguida, discute estas questões, uma vez que elas estão relacionadas a um único algoritmo: k-Nearest Neighbor. Ele então fornece algumas questões chave para pensar ao gerenciar viés e variância, incluindo técnicas de reamostragem, propriedades assimptóticas dos algoritmos e seu efeito sobre o viés e erros de variância, e combatendo as suposições de uma pessoa em relação aos dados e sua modelagem.
O ensaio termina afirmando que, em seu coração, esses 2 conceitos estão fortemente ligados tanto ao sobre quanto ao sub-ajuste. Na minha opinião, aqui está o ponto mais importante:
Como cada vez mais parâmetros são adicionados a um modelo, a complexidade do modelo sobe e a variância torna-se a nossa principal preocupação enquanto que o enviesamento cai constantemente. Por exemplo, como mais termos polinomiais são adicionados a uma regressão linear, quanto maior for a complexidade do modelo resultante. Em outras palavras, o viés tem uma derivada negativa de primeira ordem em resposta à complexidade do modelo enquanto a variância tem uma inclinação positiva.

Fig. 2: Viés e variância contribuindo para o erro total
From Understanding the Bias-Variance Tradeoff, de Scott Fortmann-Roe.
Fortmann-Roe termina a seção sobre over- and under-fitting apontando para outro de seus grandes ensaios (Accurately Measuringly Model Prediction Error), e passando então para a recomendação altamente agradável de que “medidas baseadas em reamostragem, como a validação cruzada, devem ser preferidas a medidas teóricas, como o Aikake’s Information Criteria”.
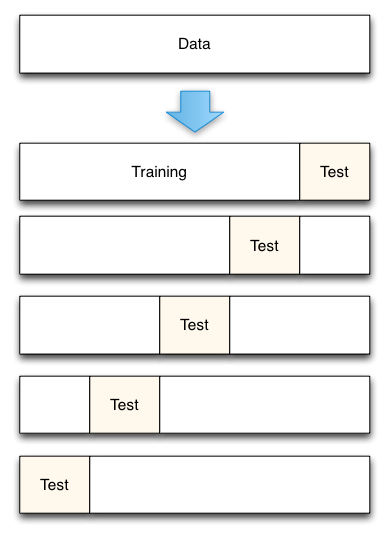
Fig. 3: Divisão de dados de validação cruzada de 5 vezes
De Accurately Measuringlyly Model Prediction Error, por Scott Fortmann-Roe.
Orção, com a validação cruzada, o número de dobras a usar (k-validação cruzada, certo?), o valor de k é uma decisão importante. Quanto menor o valor, maior o viés nas estimativas de erro e menor a variância. Por outro lado, quando k é definido igual ao número de instâncias, a estimativa de erro é então muito baixa no viés, mas tem a possibilidade de alta variância. O viés-variação é claramente importante para entender até mesmo os métodos mais rotineiros de avaliação estatística, como a validação cruzada de k-fold.
Felizmente, a validação cruzada também parece, às vezes, ter perdido seu fascínio na era moderna da ciência dos dados, mas isso é uma discussão para outra época.
Eu recomendo a leitura de todo o ensaio de Scott Fortmann-Roe sobre a variação do viés, bem como a sua peça sobre a medição do erro de predição do modelo.
Related:
- Big Data, Bible Codes, and Bonferroni
- Data Science of Variable Selection: Revisão
- Dados sobre Algoritmos
