Roteamento do Estado do Link é uma técnica em que cada roteador compartilha o conhecimento de sua vizinhança com todos os outros roteadores na internet.
As três chaves para entender o algoritmo de Roteamento do Estado do Link:
- Conhecimento sobre a vizinhança: Ao invés de enviar sua tabela de roteamento, um roteador envia as informações sobre sua vizinhança apenas. Um roteador transmite suas identidades e o custo dos links diretamente ligados a outros roteadores.
- Flooding: Cada roteador envia a informação para todos os outros roteadores na internet, exceto seus vizinhos. Este processo é conhecido como Flooding. Cada roteador que recebe o pacote envia as cópias para todos os seus vizinhos. Finalmente, cada roteador recebe uma cópia da mesma informação.
- Partilha de informação: Um roteador envia a informação para cada outro roteador somente quando a mudança ocorre na informação.
Link State Routing tem duas fases:
Inundação confiável
- Estado inicial: Cada nó sabe o custo dos seus vizinhos.
- Estado final: Cada nó conhece o gráfico inteiro.
Cálculo da rota
Cada nó usa o algoritmo de Dijkstra no gráfico para calcular as rotas ideais para todos os nós.
- O algoritmo de roteamento do Link state é também conhecido como algoritmo de Dijkstra que é usado para encontrar o caminho mais curto de um nó para cada outro nó na rede.
- O algoritmo do Dijkstra é um iterativo, e tem a propriedade de que após a kth iteração do algoritmo, os caminhos de menor custo são bem conhecidos para k nós de destino.
Deixemos descrever algumas notações:
- c( i , j): Custo da ligação do nó i ao nó j. Se i e j nós não estiverem diretamente ligados, então c(i , j) = ∞.
- D(v): Define o custo do caminho do código fonte para o destino v que tem o menor custo atualmente.
- P(v): Define o nó anterior (vizinho do v) junto com o caminho de menor custo atual do código fonte para v.
- N: É o número total de nós disponíveis na rede.
Algoritmo
InitializationN = {A} // A is a root node.for all nodes vif v adjacent to Athen D(v) = c(A,v)else D(v) = infinityloopfind w not in N such that D(w) is a minimum.Add w to NUpdate D(v) for all v adjacent to w and not in N:D(v) = min(D(v) , D(w) + c(w,v))Until all nodes in N
No algoritmo acima, um passo de inicialização é seguido pelo laço. O número de vezes que o laço é executado é igual ao número total de nós disponíveis na rede.
Deixe entender através de um exemplo:
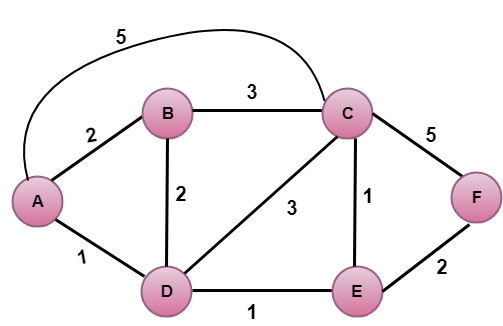
Na figura acima, o vértice fonte é A.
Passo 1:
O primeiro passo é um passo de inicialização. O caminho de menor custo atualmente conhecido de A até seus vizinhos diretamente ligados, B, C, D são 2,5,1 respectivamente. O custo de A para B é definido como 2, de A para D é definido como 1 e de A para C é definido como 5. O custo de A a E e F está definido para o infinito, pois não estão diretamente ligados a A.
| Passo | N | D(B),P(B) | D(C),P(C) | D(D),P(D) | D(E),P(E) | D(F),P(F) |
|---|---|---|---|---|---|---|
| 1 | A | 2,A | 5,A | 1,A | ∞ | ∞ |
Passo 2:
Na tabela acima, observamos que o vértice D contém o caminho de menor custo no passo 1. Portanto, ele é adicionado em N. Agora, precisamos determinar um caminho de menor custo através do vértice D.
a) Calculando o caminho mais curto de A a B
b) Calculando o caminho mais curto de A a C
c) Calculando o caminho mais curto de A a E
Nota: O vértice D não tem ligação direta com o vértice E. Portanto, o valor de D(F) é infinito.
| Passo | N | D(B),P(B) | D(C),P(C) | D(D),P(D) | D(E),P(E) | D(F),P(F) |
|---|---|---|---|---|---|---|
| 1 | A | 2,A | 5,A | 1,A | ∞ | ∞ |
| 2 | AD | 2,A | 4,D | 2,D | ∞ |
Passo 3:
Na tabela acima, observamos que tanto E como B têm o caminho de menor custo no passo 2. Vamos considerar o vértice E. Agora, determinamos o caminho de menor custo dos vértices restantes através de E.
a) Calculando o caminho mais curto de A a B.
b) Calculando o caminho mais curto de A a C.
c) Calculando o caminho mais curto de A a F.
| Passo | N | D(B),P(B) | D(C),P(C) | D(D),P(D) | D(E),P(E) | D(F),P(F) | ||
|---|---|---|---|---|---|---|---|---|
| 1 | A | 2,A | 5,A | 1,A | ∞ | ∞ | ||
| 2 | AD | AD | 2,A | 4,D | 2,D | ∞ | ||
| 3 | ADE | 2,A | 3,E | 4,E |
Step 4:
Na tabela acima, observamos que o vértice B tem o caminho de menor custo no passo 3. Portanto, ele é adicionado em N. Agora, nós determinamos o caminho de menor custo dos vértices restantes através de B.
a) Calculando o caminho mais curto de A a C.
b) Calculando o caminho mais curto de A a F.
| Passo | N | D(B),P(B) | D(C),P(C) | D(D),P(D) | D(E),P(E) | D(F),P(F) | |||
|---|---|---|---|---|---|---|---|---|---|
| 1 | A | 2,A | 5,A | 1,A | ∞ | ∞ | |||
| 2 | AD | 2,A | 4,D | 2,D | ∞ | ||||
| 3> | > | 2,A | 3,A | 3,E | 4,E | ||||
| 4 | ADEB | 3> | 3,E | 4,E |
Step 5:
Na tabela acima, observamos que o vértice C tem o caminho de menor custo no passo 4. Portanto, ele é adicionado em N. Agora, nós determinamos o caminho de menor custo dos vértices restantes através de C.
a) Calculando o caminho mais curto de A a F.
| Passo | N | D(B),P(B) | D(C),P(C) | D(D),P(D) | D(E),P(E) | D(F),P(F) | |||
|---|---|---|---|---|---|---|---|---|---|
| 1 | A | 2,A | 5,A | 1,A | ∞ | ∞ | |||
| 2 | AD | 2,A | 4,D | 2,D | ∞ | ||||
| 3 | ADE | 2,A | 3,E | 4,E | |||||
| 4 | ADEB | 3,E | > | 4,E | |||||
| 5 | ADEBC | 4,E |
Tabela final:
| Passo | N | D(B),P(B) | D(C),P(C) | D(D),P(D) | D(E),P(E) | D(F),P(F) | |
|---|---|---|---|---|---|---|---|
| 1 | A | 2,A | 5,A | 1,A | ∞ | ∞ | |
| 2 | AD | 2,A | 4,D | 2,D | ∞ | ||
| 3 | ADE | 2,A | 3,E | 4,E | |||
| 4 | ADEB | 3,E | 4,E | ||||
| >5 | ADEBC | 4,E | |||||
| >6 | ADEBCF |
Desvantagem:
Tráfego pesado é criado no roteamento de estado de linha devido a Inundação. Inundação pode causar um looping infinito, este problema pode ser resolvido usando o campo Time-to-leave
