A estimulação de tempo, esforços e custos é uma das partes mais críticas da gestão de projectos. Isso se deve à importância fundamental dessas estimativas para todo o planejamento do projeto e, em particular, para o escopo, o cronograma e a linha de base de custos. Uma das técnicas de estimação sugeridas no Project Management Body of Knowledge do PMI (PMBOK 6th ed., cap. 6.4, 7.2) é a estimativa de três pontos usada com a distribuição triangular, Beta ou PERT. Vamos introduzir estes métodos neste artigo.
Qual é a Técnica de Estimação de Três Pontos?
A estimativa de três pontos é uma abordagem simples mas útil para estimar o tempo ou o custo dos itens de trabalho. De acordo com a metodologia PMI, ela é usada nos grupos de processo “Estimar Duração da Atividade” e “Estimar Custos”. A técnica envolve três estimativas diferentes que normalmente são obtidas de especialistas no assunto:
- Estimativa otimista,
- Estimativa pessimista,
- Estimativa mais provável.
A estimativa otimista é a quantidade esperada de trabalho ou tempo necessário para realizar uma atividade, assumindo que não ocorram impedimentos e que tudo esteja indo bem. Ela representa o chamado melhor cenário possível. O ponto pessimista é baseado no pressuposto de que o oposto foi verdadeiro – representa o pior cenário possível. Embora ambas as estimativas estejam se referindo aos pontos extremos da gama de resultados esperados, as estimativas são supostamente um pouco realistas.
O terceiro ponto reflete o caso mais provável, é a estimativa de trabalho ou tempo que é considerado o mais realista. Poderíamos ser tentados a simplesmente usar a média entre os pontos otimista e pessimista sem dar uma segunda reflexão. No entanto, isto pode não ser apropriado para muitos casos. Na prática, normalmente vale a pena determinar esta estimativa mais provável, análoga aos outros pontos de estimativa.
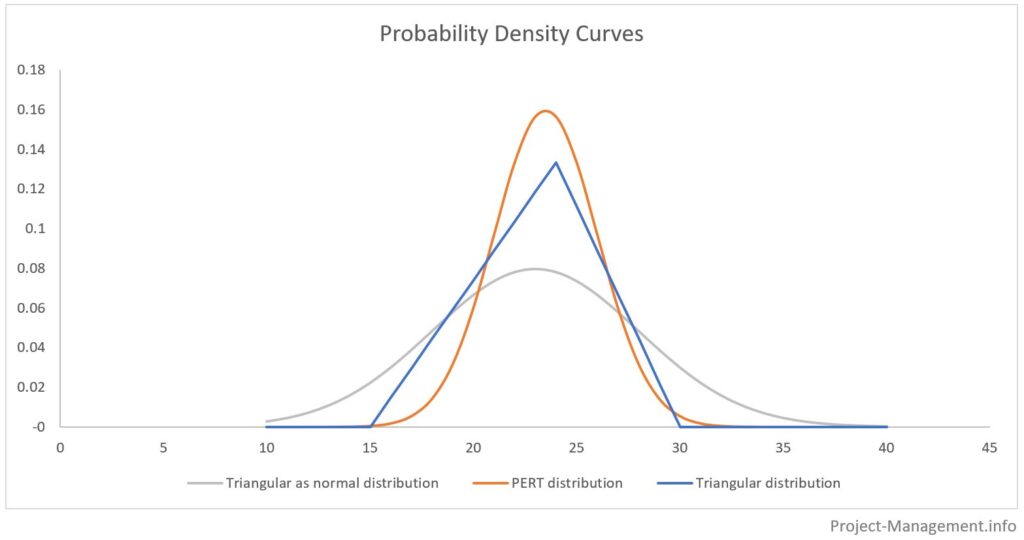
O resultado da estimativa de três pontos é uma distribuição triangular de valores de tempo ou valores de custo, compreendendo as três estimativas (ver ilustração abaixo).
O que é PERT?
PERT significa Técnica de Avaliação e Revisão de Programas e foi desenvolvido como um sistema avançado de planejamento e gerenciamento de cronograma de projetos pela marinha americana nos anos 50 (fonte: Heldman, PMP Study guide, cap. 4).
Outra história, não muito séria, de sua origem foi publicada uma vez por um autor anônimo na revista do PMI (Link; fonte: Anônimo (1975). PERT – o embuste do século. Project Management Quarterly, 6(3), 22-23).
Em projetos estilo PMI, o PERT é usado principalmente como uma técnica suplementar ao Método do Caminho Crítico para atividades de agendamento. Entretanto, ele também pode ser aplicado a estimativas isoladas de workitems e atividades.
A chamada distribuição PERT alavanca os valores determinados com a técnica de estimativa de três pontos. Ela pode ser usada basicamente para todos os níveis de planejamento, desde atividades até projetos inteiros. Entretanto, encontrar a granularidade certa para uma estimativa significativa pode exigir algum pensamento crítico e conceitual.
O método PERT implica sobrepeso da estimativa “mais provável”. Ele transforma a estimativa de três pontos em curva em forma de abelha e permite determinar probabilidades de intervalos de valores esperados.
Quais são as diferenças entre a distribuição triangular e a distribuição PERTD das estimativas de três pontos?
Embora a distribuição triangular apenas consista nos três pontos estimados, o método PERT permite converter a estimativa de três pontos numa curva em forma de sino, quase normalmente distribuída.
As áreas sob as curvas de distribuição de probabilidade representam as probabilidades acumuladas dos respectivos intervalos de estimativas. Normalmente, estes intervalos são determinados com o valor esperado +/- desvio padrão multiplicado por 1, 2 e 3. Isto é ilustrado na seguinte figura:
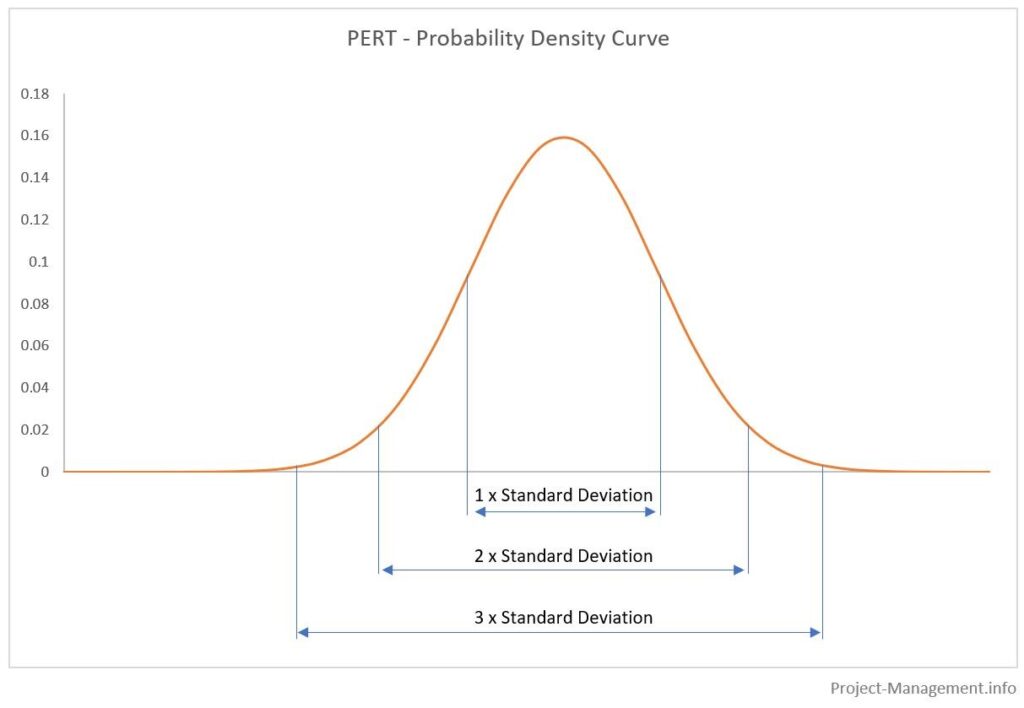
As probabilidades resultantes (aprox.) são
- 68,3% para 1 desvio padrão,
- 95.5% para 2 desvios padrão,
- 99,7% para 3 desvios padrão,
O conhecimento necessário para o exame PMP é limitado ao cálculo das estimativas esperadas e à familiaridade com as diferentes probabilidades (fonte). Portanto, não iremos cobrir os detalhes estatísticos e o histórico neste artigo – você pode encontrar esses detalhes no Riskamp.
Utilize essa calculadora para determinar as estimativas de três pontos e PERT.
Como é calculada a estimativa de três pontos?
A distribuição triangular
O cálculo simples mas comumente usado envolve a média ou média dos 3 valores estimados. A fórmula desta distribuição triangular é:
E =(O + M + P) / 3
where:
E = Tempo ou custo esperado,
O = Estimativa otimista,
M = Estimativa mais provável,
P = Estimativa pessimista.
O PMBOK usa t(E), t(O), t(M) e t(P) asvariáveis para estimativas de tempo e c(E), c(O), c(M) e c(P).
O peso de cada estimativa na sequência é idêntico. Assim, o caso ‘mais provável’ não afeta a estimativa final mais do que as 2 estimativas menos prováveis. Isto é diferente do método de betadistribuição.
A Distribuição Beta PERT
A distribuição beta PERT leva em conta que o caso ‘mais provável’ é mais provável de ocorrer, o que é reflectido num multiplicador para essa estimativa. A metodologia PMI sugere este cálculo como uma alternativa à distribuição triangular para estimativas de custos (entretanto, somos da opinião de que ela também pode ser usada para estimativas de tempo).
Neste método, o estimador mais provável obtém um multiplicador de 4 enquanto o divisor geral é aumentado para 6. A fórmula é a seguinte:
E =(O + 4*M + P) / 6
where:
E = Tempo ou custo esperado,
O = Estimativa otimista,
M = Estimativa mais provável,
P = Estimativa pessimista.
O desvio padrão da distribuição PERT é calculado usando a fórmula:
Desvio Padrão = (P – O) / 6
Para estimar um caminho inteiro (método do caminho analógico crítico), um conceito similar é aplicado ainda usando um desvio padrão combinado de todas as atividades.
Exemplo de uma estimativa de três pontos e PERT
Uma equipe de especialistas no assunto está avaliando o tempo que leva para completar uma atividade. Neste exemplo, a duração de uma actividade é estimada utilizando a técnica de estimativa de três pontos.Eles apresentam os seguintes números:
| Estimativa otimista | 15 dias |
| Estimativa pessimista | 24 dias |
| Estimativa mais provável | 30 dias |
Os valores variam de 15 dias (optimista)a 30 dias (pessimista). Uma duração de 24 dias é considerada como o tempo mais provável necessário para a conclusão do trabalho.
Cálculo da duração esperada com uma distribuição triangular
A duração esperada usando uma distribuição triangular é calculada da seguinte forma:
FinalEstimate = (15 + 30 + 24) / 3.
A estimativa final resultante sob este método é 23, que é basicamente a média não ponderada das 3 estimativas.
Cálculo da Duração Esperada Usando a Distribuição PERT BetaDistribuição
A duração esperada também pode ser calculada com o método PERT:
Estimativa Final (valor esperado) = (15 + 4×24 + 30) / 6.
O valor esperado resultante é 23,5 dias, que é maior do que a estimativa final determinada pelo método triangular. Isto é devido ao maior peso (ou seja, multiplicador de 4) que é atribuído à estimativa ‘mais provável’.
O desvio padrão desta estimativa é:
DesvioPadrão = (30 – 15) / 6 = 2,5
Determinando as Probabilidades da Duração Esperada
A poupança calculada a duração esperada e o desvio padrão permite ao gestor do projecto determinar as probabilidades (aprox.):
| Alcance | Probabilidade | Limite Inferior | Limite Superior |
| 1 x desvio padrão | 68.3% | 21 | 26 |
| 2 x desvio padrão | 18,5 | 28,5 | |
| 3 x desvio padrão | 99.7% | 31 |
Com 68,3% de probabilidade, a duração da atividade será entre 21 e 26 dias. Para um intervalo de 18,5 a 28,5 dias, a probabilidade é de 95,5%. Usando 3 desvios padrão cobre quase todos os pontos de dados e determina uma probabilidade de 99,7% de que a duração seja entre 16 e 31 dias.
Sumário
A estimativa final sob o método triangular foi 23, comparado a 23,5 usando o método PERT. Isto porque a matéria atribui uma pesagem mais elevada ao caso ‘mais provável’ que, no nosso caso, não é exactamente a média (ou média não ponderada) da estimativa optimista e pessimista.
Utilizar o método PERT permite ter em conta as probabilidades dos intervalos de valores. Isto é útil se a qualidade das estimativas variar, por exemplo, se a diferença entre as estimativas otimista e pessimista estiver se desviando significativamente entre diferentes atividades. Neste caso, a utilização de intervalos e suas probabilidades irá refletir a dispersão e o nível de confiança das estimativas subjacentes.
Conclusão
A estimativa de atividades com respeito às suas necessidades de tempo e custo é crucial para o planejamento e programação dos projetos e atividades. Em muitos projetos, estimativas mais precisas, tais como estimativas paramétricas, baseadas em correlações estatísticas de projetos comparáveis no passado, por exemplo, não estão disponíveis. A técnica de estimativa de três pontos oferece uma boa abordagem para processar e equilibrar estimativas top-down ou estimativas de especialistas em tais situações.
A distribuição PERT é provavelmente o método mostaccura para agregar estes piores, melhores e mais prováveis casos em números isolados (valor esperado) ou uma gama de valores. Graças ao uso do desvio-padrão, ele leva em conta tanto as incertezas inerentes quanto a dispersão potencial das estimativas.
Esta pode ser a razão pela qual o PERT ainda é um método comum na estimativa e agendamento de projetos, embora já exista há algumas décadas e já pudesse ter sido usado pelos nossos avós (se eles tivessem sido gestores de projeto).
