Introdução :
Similaridade Cosina é usada para determinar a similaridade entre documentos ou vetores. Matematicamente, mede o cosseno do ângulo entre dois vetores projetados em um espaço multidimensional. Existem outras técnicas de medição de similaridade como a distância Euclidiana ou a distância de Manhattan disponíveis, mas estaremos focando aqui na Similaridade Cosina e na Distância Cossina.
A relação entre semelhança cosseno e distância cosseno pode ser definida como abaixo.
- Similaridade diminui quando a distância entre dois vectores aumenta

>
2. A semelhança aumenta quando a distância entre dois vectores diminui.

Semelhança Cosina e Distância Cosina:
Semelhança Cosina diz que para encontrar a semelhança entre dois pontos ou vectores precisamos de encontrar o ângulo entre eles.
Fórmula para encontrar a Similaridade Cosina e a Distância é como abaixo:


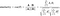
Aqui A=Ponto P1,B=Ponto P2 (no nosso exemplo)
Vejamos os vários valores de Cos Θ para entender a semelhança cosseno e a distância cosseno entre dois pontos de dados(vectores) P1 & P2 considerando dois eixos X e Y.
Below Picture tendo aí Casos.
Caso 1: Quando o ângulo entre os pontos P1 & P2 é 45 Grau então
cosine_similarity= Cos 45 = 0.525
Caso 2: Quando dois pontos P1 & P2 estão longe um do outro e o ângulo entre os pontos é 90 Grau então
cosine_similarity= Cos 90 = 0
Caso 3: Quando dois pontos P1 & P2 estão muito próximos e estão no mesmo eixo um do outro e o ângulo entre os pontos é de 0 Grau então
>
cosine_similarity= Cos 0 = 1
>
 >
>>>
>
>
Below Picture tendo os próximos três casos.
Caso 4: Quando os pontos P1 & P2 estão em frente um do outro e o ângulo entre os pontos é de 180º então
cosine_similarity= Cos 180 = -1
Caso 5: Quando o ângulo entre os pontos P1 & P2 é de 270º então
cosine_similarity= Cos 270 = 0
Caso 6: Quando o ângulo entre os pontos P1 & P2 é 360 Grau então
cosine_similarity= Cos 360 = 1

Passemos estes valores de cada ângulo discutido acima e vejamos a Distância Cosine entre dois pontos.
1 – Cosine_Similarity=Cosine_Distance
Caso 1: Quando Cos 45 Graus
Vamos substituir os valores da fórmula acima .
1-0.525=Cosine_Distance
0.475 =Cosine_Distance
Case 2: Quando Cos 90 Graus
1-0= Cosine_Distance
1 =Cosine_Distance
Case 3: Quando Cos 0 Grau
1-1= Cosine_Distance
0 =Cosine_Distance
Case 4: When Cos 180 Degree
1-(-1)= Coseno_Distância
2 =Coseno_Distância
Caso 5: When Cos 270 Degree
1-0= Coseno_Distância
1 =Coseno_Distância
Caso 6: When Cos 360 Degree
1-1= Cosine_Distance
0 =Cosine_Distance
Vemos claramente que quando a distância é menor a semelhança é mais (os pontos estão próximos um do outro) e a distância é mais, dois pontos são diferentes (longe um do outro)
Cosine Similarity and Cosine Distance é muito utilizado em sistemas de recomendação para recomendar produtos aos utilizadores com base nos gostos e aversões dos mesmos.
Poucos exemplos onde isto é usado são websites como Amazon,Flipkart para recomendar itens aos clientes para experiência personalizada,Classificação e recomendação de filmes etc.
Conclusão : Espero que por esta altura já tenham um claro entendimento da matemática por detrás do cálculo da semelhança cosseno e da distância cosseno e do seu uso.
Espera que gostem do meu artigo.Por favor carreguem na aba 👏(50 vezes) para me motivarem a escrever mais.
Quer ligar-se :
Linked In : https://www.linkedin.com/in/anjani-kumar-9b969a39/
Se você gosta dos meus posts aqui no Medium e gostaria que eu continuasse a fazer este trabalho, considere apoiar-me no patreon
