En standardavvikelse är ett tal som talar om i vilken utsträckning en uppsättning tal ligger isär.En standardavvikelse kan sträcka sig från 0 till oändligt. En standardavvikelse på 0 innebär att en lista med siffror är lika – de ligger inte isär i någon utsträckning alls.
Standardavvikelse – exempel
Fem sökande gjorde ett IQ-test som en del av en jobbansökan. Deras resultat på tre IQ-komponenter visas nedan.
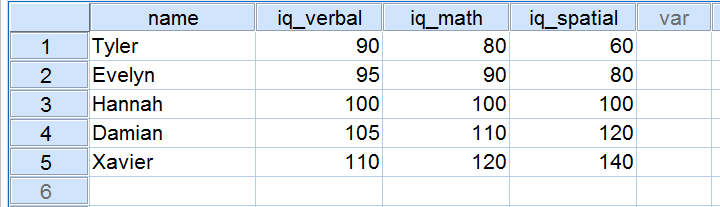
Nu ska vi titta närmare på resultaten på de tre IQ-komponenterna. Observera att alla tre har ett medelvärde på 100 för våra fem sökande. Poängen för iq_verbal ligger dock närmare varandra än poängen för iq_math. Dessutom ligger poängen för iq_spatial längre ifrån varandra än poängen för de två första komponenterna. Den exakta omfattningen av hur långt ett antal poäng ligger ifrån varandra kan uttryckas som ett tal. Detta tal kallas standardavvikelse.
Standardavvikelse – Resultat
I verkligheten inspekterar vi naturligtvis inte visuellt råpoängen för att se hur långt de ligger ifrån varandra. I stället låter vi helt enkelt någon programvara beräkna dem åt oss (mer om det senare). Tabellen nedan visar standardavvikelserna och lite annan statistik för våra IQ-data. Observera att standardavvikelserna bekräftar det mönster vi såg i rådata.
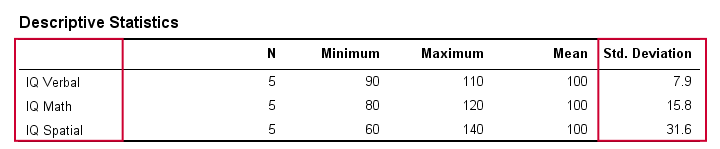
Standardavvikelse och histogram
Okej, låt oss göra det hela lite mer visuellt. Figuren nedan visar standardavvikelserna och histogrammen för våra IQ-poäng. Observera att varje stapel representerar poängen för 1 sökande på 1 IQ-komponent. Återigen ser vi att standardavvikelserna visar i vilken utsträckning poängen ligger isär.
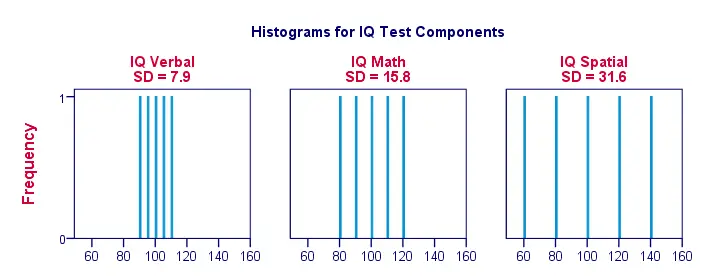
Standardavvikelse – fler histogram
När vi visualiserar data på bara en handfull observationer som i den föregående figuren ser vi lätt en tydlig bild. För ett mer realistiskt exempel presenterar vi histogram för 1 000 observationer nedan. Viktigt är att dessa histogram har identiska skalor; för varje histogram motsvarar en centimeter på x-axeln cirka 40 ”IQ-komponentpunkter”.
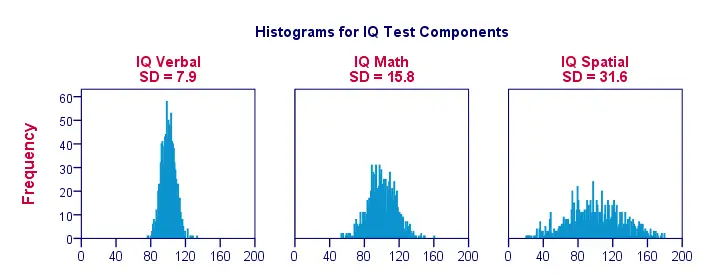
Bemärk hur histogrammen möjliggör grova uppskattningar av standardavvikelser. ”Bredare” histogram tyder på större standardavvikelser; poängen (x-axeln) ligger längre ifrån varandra. Eftersom alla histogram har identiska ytor (motsvarande 1 000 observationer) är större standardavvikelser också förknippade med ”bredare” histogram.
Standardavvikelse – befolkningsformel
Hur beräknar din programvara standardavvikelser? Den grundläggande formeln är
$$$\sigma = \sqrt{\frac{\sum(X – \mu)^2}{N}}}$$$
där
- \(X\) betecknar varje separat tal;
- \(\mu\) betecknar medelvärdet över alla tal och
- \(\sum\) betecknar en summa.
Med andra ord är standardavvikelsen kvadratroten av den genomsnittliga kvadratiska skillnaden mellan varje enskilt tal och medelvärdet av dessa tal.
Väsentligt är att denna formel förutsätter att dina data innehåller hela den intressanta populationen (därav ”populationsformel”). Om dina data endast innehåller ett urval av din målpopulation, se nedan.
Populationsformel – Programvara
Du kan använda den här formeln i Google ark, OpenOffice och Excel genom att skriva =STDEVP(...) i en cell. Ange de siffror över vilka du vill ha standardavvikelsen mellan parenteserna och tryck på Enter. Figuren nedan illustrerar idén.
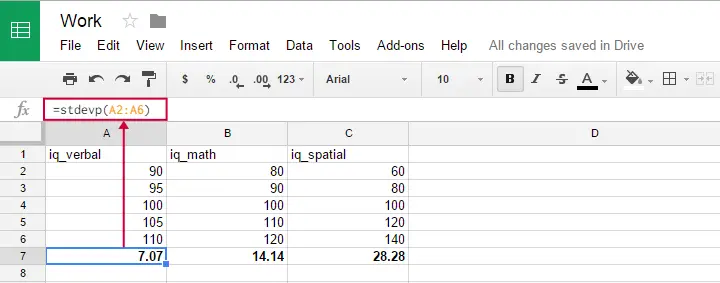
Märkligt nog verkar inte formeln för populationsstandardavvikelse finnas i SPSS.
Standardavvikelse – formel för stickprov
Nu kommer vi till något utmanande: om dina data är (ungefär) ett enkelt slumpmässigt stickprov från en (mycket) större population, så kommer den tidigare formeln systematiskt att underskatta standardavvikelsen i denna population. En fördomsfri skattare för populationens standardavvikelse erhålls genom att använda
$$$$S_x = \sqrt{\frac{\sum(X – \overline{X})^2}{N -1}}}$$
När det gäller beräkningar är den stora skillnaden mot den första formeln att vi dividerar med \(n -1\) istället för \(n\). Att dividera med ett mindre tal ger ett (något) större resultat. Detta kompenserar just för den tidigare nämnda underskattningen. För stora urvalsstorlekar har dock de två formlerna praktiskt taget identiska resultat.
I GoogleSheets, Open Office och MS Excel använder STDEV-funktionen denna andra formel. Det är också den (enda) formeln för standardavvikelse som implementerats i SPSS.
Standardavvikelse och varians
Ett andra tal som uttrycker hur långt en uppsättning tal ligger ifrån varandra är variansen. Variansen är den kvadrerade standardavvikelsen. Detta innebär att variansen, på samma sätt som standardavvikelsen, har en populationsformel såväl som en stickprovsformel.
I princip är det besvärligt att två olika statistiska mått i princip uttrycker samma egenskap hos en uppsättning tal. Varför inte bara slänga variansen till förmån för standardavvikelsen (eller tvärtom)? Det grundläggande svaret är att standardavvikelsen har mer önskvärda egenskaper i vissa situationer och variansen i andra.
