Tillämpning av Buckingham Pi-satsen

Nästa: Upp: Buckingham Pi-sats Föregående: Buckingham Pi-sats

Användning av Buckingham Pi-sats

Den sats som vi har angivit är mycket allmän, men på intet sätt begränsad till strömningsmekanik. Den används inom många olika områden, t.ex. botanik och samhällsvetenskap, och böcker och volymer har skrivits om detta ämne. Men vi behöver inte mycket teori för att kunna tillämpa den. Vad vi kommer att överväga är ett förfarande för att använda teoremet och komma fram till icke-dimensionella tal för ett givet flöde.

1. Lista alla variabler som styr processen. Dessa variabler bör vara oberoende av varandra. Man bör till exempel inte välja densitet, gravitation och specifik vikt. Densitet och specifik vikt bör räcka. För vårt problem har vi F, D, V, och . Vi har n = 5.
2. Märk de upprepande variablerna. I vårt fall är dessa D, V och vilket gör att k = 3 .
3. Beslut hur många icke-dimensionella tal det finns. I vårt fall har vi n – k = 2. Vårt problem har 2 icke-dimensionella tal, och .
4. Definiera de icke-dimensionella talen genom att gruppera variablerna i n – k grupper så att varje grupp har alla upprepande variabler och en icke upprepande variabel. För vårt problem har vi alltså

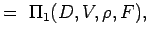
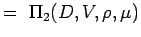
   		(5.2)
   Let
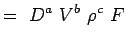
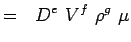
   		(5.3)

5. Uttryck nu varje variabel i termer av dess dimensioner. Låt oss använda MLT-systemet enligt vilket variablerna för våra problem har följande dimensioner.
   

   Variabel	Dimensioner
   F, Kraft	M L / T2 eller M L T-2
   D, Diameter:	L
   V, Hastighet	L/T eller LT-1
   , Densitet:	M/L3 eller ML-3
   , Viskositet	ML-1T-1

   Substituera dessa dimensioner i Eqn. 5.2 har vi

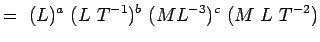
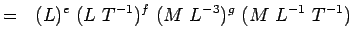
   		(5.4)
   Och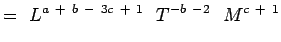
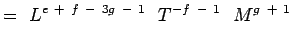
   		(5.5)

   Med tanke på att och är icke-dimensionella har vi,

   a + b – 3c + 1 = 0; -b – 2 = 0, c + 1 = 0
   e + f – 3g – 1 = 0; -f – 1 = 0;g + 1 = 0	(5.6)

   Lösning av ekvationerna ger,

   a = -2, b = -2, c = -1
   e = -1, f = -1, g = -1	(5.7)

   Nu blir våra icke-dimensionella tal,

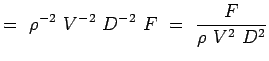
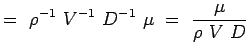
   		(5.8)

Därmed har vi funnit de icke-dimensionella talen för det aktuella flödet, nämligen dragningen runt en cirkulär cylinder. Det funktionella sambandet mellan de två talen kan uttryckas som

Men observera att formen för termen som vi har härlett är något annorlunda än vad vi antog i början. Den högra sidan av ekvationen är i själva verket den omvända delen av Reynolds tal!Detta visar på nackdelen med analysen att den exakta funktionella formen mellan talen inte kan erhållas. Alla koefficienter eller index som erhålls kan inte bestämmas genom denna analys. Detta bör bestämmas genom experiment eller beräkningar. Men eftersom siffrorna är icke-dimensionella kan vi skriva

nästa: Upp: Buckingham Pi-sats Föregående: Buckingham Pi-sats

(c) Aerospace, Mechanical & Mechatronic Eng. 2005
University of Sydney