Att beräkna tid, insatser och kostnader är en av de mest kritiska delarna av projektledning. Detta beror på den grundläggande betydelsen av dessa uppskattningar för hela projektplaneringen och i synnerhet för baslinjen för omfattning, tidsplan och kostnader. En av de uppskattningstekniker som föreslås i PMI Project Management Body of Knowledge (PMBOK 6th ed., kap. 6.4, 7.2) är trepunktsberäkningen som används med triangel-, beta- eller PERT-fördelningen. Vi kommer att presentera dessa metoder i den här artikeln.
Vad är trepunktsskattningstekniken?
Trepunktsskattningen är ett enkelt men användbart tillvägagångssätt för att uppskatta tiden eller kostnaden för arbetsmoment. Enligt PMI-metodiken används den i processgrupperna ”Estimate Activity Duration” och ”Estimate Costs”. Tekniken innefattar tre olika uppskattningar som vanligtvis erhålls från ämnesexperter:
- Optimistisk uppskattning,
- Pessimistisk uppskattning,
- Mest trolig uppskattning.
Den optimistiska uppskattningen är den förväntade arbetsmängden eller tidsåtgången som behövs för att utföra en aktivitet, om man antar att inga hinder uppstår och att allt går smidigt. Den representerar det så kallade bästa tänkbara scenariot. Den pessimistiska punkten bygger på antagandet att det motsatta skulle vara sant – den representerar det värsta scenariot. Även om båda uppskattningarna hänvisar till de extrema punkterna i intervallet av förväntade resultat, antas uppskattningarna vara någorlunda realistiska.
Den tredje punkten återspeglar det mest sannolika fallet, det är den uppskattning av arbete eller tid som anses vara den mest realistiska. Man kan frestas att helt enkelt använda medelvärdet mellan den optimistiska och den pessimistiska punkten utan att tänka efter. Detta kan dock vara olämpligt i många fall. I praktiken är det normalt sett värt att bestämma denna mest sannolika uppskattning ordentligt, analogt med de andra uppskattningspunkterna.
Resultatet av trepunktsberäkning är en så kallad triangulär fördelning av tidsvärden eller kostnadsbelopp, bestående av de tre uppskattningarna (se illustrationen nedan).
Vad är PERT?
PERT står för Program Evaluation and Review Technique och utvecklades som ett avancerat system för planering och hantering av projektplaner av den amerikanska flottan på 1950-talet (källa: Heldman, PMP Study guide, kap. 4).
En annan, inte alltför allvarlig, berättelse om dess tillkomst publicerades en gång av en anonym författare i PMI:s tidskrift (Link; källa: Anonym (1975). PERT-the hoax of the century. Project Management Quarterly, 6(3), 22-23).
I projekt i PMI-stil används PERT i första hand som en kompletterande teknik till Critical Path Method för planering av aktiviteter. Den kan dock också tillämpas på fristående uppskattningar av arbetsmoment och aktiviteter.
Den så kallade PERT-fördelningen bygger på de värden som fastställts med hjälp av trepunktsmetoden för uppskattning. Den kan i princip användas för alla planeringsnivåer, från aktiviteter till hela projekt. Det kan dock krävas en del kritiskt och konceptuellt tänkande för att hitta rätt granularitet för en meningsfull uppskattning.
PERT-metoden innebär att man överviktar den ”mest sannolika” uppskattningen. Den omvandlar trepunktsskattningen till en klockformad kurva och gör det möjligt att bestämma sannolikheterna för intervall av förväntade värden.
Vad är skillnaderna mellan triangulär och PERT-fördelning av trepunktsskattningar?
Medan den triangulära fördelningen endast tar hänsyn till de tre skattade punkterna, gör PERT-metoden det möjligt att omvandla trepunktsskattningen till en klockformad, nästan normalfördelad kurva och kan därför användas för att beräkna sannolikheterna för intervall av förväntade värden.
Följande diagram illustrerar skillnaderna mellan PERT-fördelningen, den triangulära fördelningen och en framställning av trepunktsskattningen som om den vore en normalfördelning.
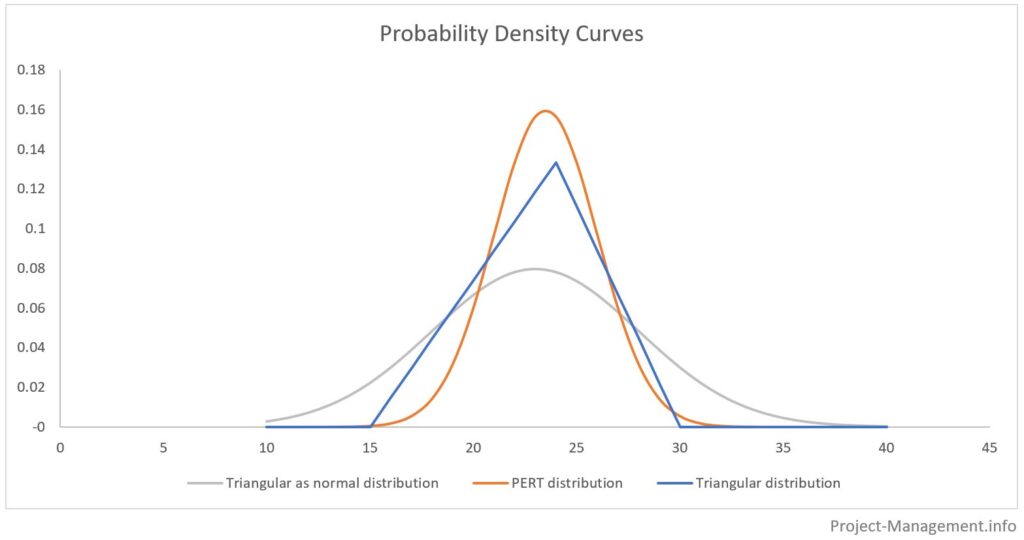
Områdena under sannolikhetsfördelningskurvorna representerar de kumulativa sannolikheterna för de respektive intervallerna av skattningar. Typiskt sett bestäms dessa intervall med det förväntade värdet +/- standardavvikelsen multiplicerat med 1, 2 och 3. Detta illustreras i följande figur:
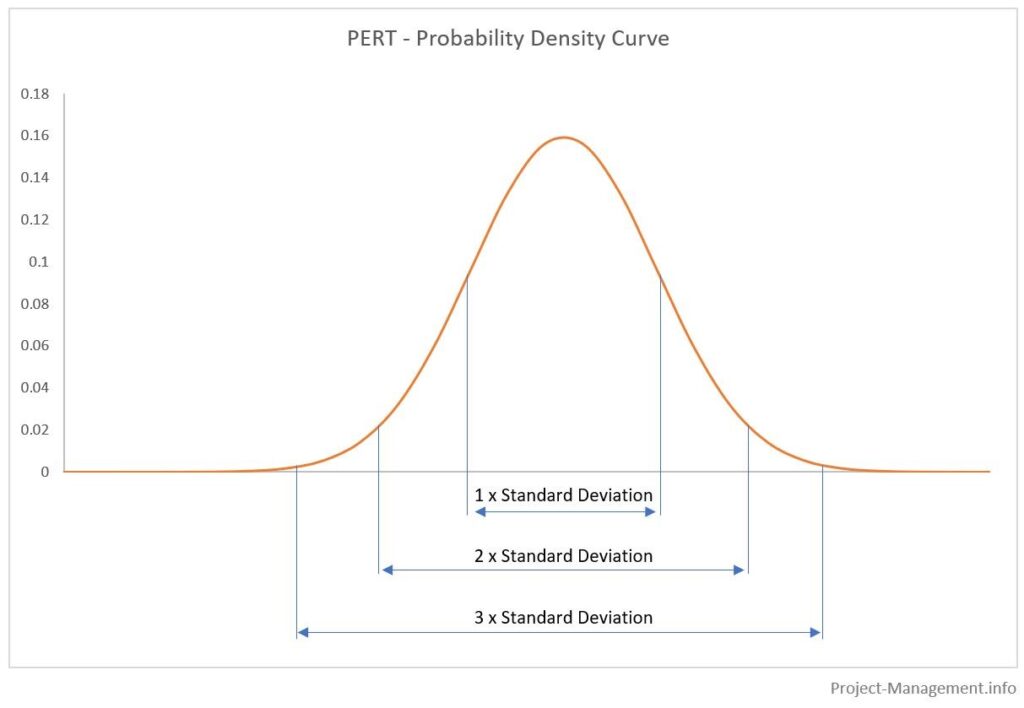
De resulterande sannolikheterna (ungefär) är
- 68,3 % för 1 standardavvikelse,
- 95.5% för 2 standardavvikelser,
- 99,7% för 3 standardavvikelser.
Den kunskap som krävs för PMP-examen är begränsad till att beräkna de förväntade skattningarna och känna till de olika sannolikheterna (källa). Därför kommer vi inte att täcka de statistiska detaljerna och bakgrunden i den här artikeln – du kan hitta dessa detaljer på Riskamp.
Använd den här kalkylatorn för att bestämma trepunktsskattningar och PERT.
Hur beräknas trepunktsskattningen?
Den triangulära fördelningen
Den enkla men ändå vanligaste beräkningen involverar genomsnittet eller medeltalet av de 3 uppskattade värdena. Formeln för denna triangelfördelning är:
E =(O + M + P) / 3
där:
E = förväntad tidsåtgång eller kostnad,
O = optimistisk uppskattning,
M = mest sannolik uppskattning,
P = pessimistisk uppskattning.
PMBOK använder t(E), t(O), t(M) och t(P) som variabler för tidsuppskattningar och c(E), c(O), c(M) och c(P).
Viktningen av varje uppskattning i denna ekvation är identisk. Det ”mest sannolika” fallet påverkar alltså inte den slutliga uppskattningen mer än de två mindre sannolika uppskattningarna. Detta skiljer sig från betafördelningsmetoden.
Perts betafördelning
Perts betafördelning tar hänsyn till att det ”mest sannolika” fallet är mer sannolikt att inträffa, vilket återspeglas i en multiplikator för den uppskattningen. I PMI-metodiken föreslås denna beräkning som ett alternativ till den triangulära fördelningen för kostnadsberäkningar (vi anser dock att den också kan användas för tidsberäkningar).
I denna metod får den mest sannolika beräkningen en multiplikator på 4 medan den totala divisorn ökas till 6. Formeln är följande:
E =(O + 4*M + P) / 6
där:
E = Förväntad tidsåtgång eller kostnad,
O = Optimistisk uppskattning,
M = Mest sannolika uppskattning,
P = Pessimistisk uppskattning.
Standardavvikelsen för PERT-fördelningen beräknas med hjälp av formeln:
Standardavvikelse = (P – O) / 6
För uppskattning av en hel sträcka (analog kritisk sträcka-metod) tillämpas ett liknande koncept, men man använder en kombinerad standardavvikelse för alla aktiviteter.
Exempel på en trepunktsberäkning och PERT
En grupp sakkunniga uppskattar den tid det tar att slutföra en aktivitet. I det här exemplet uppskattas aktivitetslängden med hjälp av trepunktsmetoden.De kommer fram till följande siffror:
| 15 dagar | |
| Pessimistisk uppskattning | 24 dagar |
| Troligast uppskattning | 30 dagar |
Värdena sträcker sig från 15 dagar (optimistisk) till 30 dagar (pessimistisk). En varaktighet på 24 dagar anses vara den mest sannolikatiden som behövs för att slutföra arbetet.
Beräkning av den förväntade varaktigheten med en triangulärfördelning
Den förväntade varaktigheten med hjälp av en triangulärfördelning beräknas på följande sätt:
Slutuppskattning = (15 + 30 + 24) / 3.
Den resulterande slutuppskattningen med denna metod är 23, vilket i princip är ett oviktat medelvärde av de tre uppskattningarna.
Beräkning av den förväntade varaktigheten med hjälp av PERT BetaDistribution
Den förväntade varaktigheten kan också beräknas med PERT-metoden:
Slutskattning (förväntat värde) = (15 + 4×24 + 30) / 6.
Det resulterande förväntade värdet är 23,5 dagar, vilket är större än den slutliga uppskattning som bestämts enligt triangulärmetoden. Detta beror på den högre vikt (dvs. multiplikatorn 4) som tilldelas den ”mest sannolika” uppskattningen.
Standardavvikelsen för denna uppskattning är:
Standardavvikelse = (30 – 15) / 6 = 2,5
Bestämning av sannolikheterna för den förväntade varaktigheten
När den förväntade varaktigheten och standardavvikelsen har beräknats kan projektledaren bestämma sannolikheterna (ca.):
| Intervall | Sannolikhet | Nedre gräns | Övre gräns |
| 1 x standardavvikelse | 68.3% | 26 | |
| 2 x standardavvikelse | 95.5% | 28.5 | |
| 3 x standardavvikelse | 99.7% | 31 |
Med 68,3 % sannolikhet kommer aktiviteten att vara mellan 21 och 26 dagar. För ett intervall mellan 18,5 och 28,5 dagar är sannolikheten 95,5 %. Om man använder tre standardavvikelser täcker man nästan alla datapunkter och fastställer en sannolikhet på 99,7 % att varaktigheten slutligen kommer att ligga mellan 16 och 31 dagar.
Sammanfattning
Den slutliga uppskattningen enligt triangulärmetoden var 23, jämfört med 23,5 enligt PERT-metoden. Detta beror på att den sistnämnda metoden ger en högre vikt åt det ”mest sannolika” fallet som i vårt fall inte är exakt medelvärdet (eller det ovägda genomsnittet av den optimistiska och den pessimistiska uppskattningen).
Användning av PERT-metoden gör det möjligt att ta hänsyn till sannolikheterna för värdeintervall. Detta är användbart om kvaliteten på uppskattningarna varierar, t.ex. om skillnaden mellan optimistiska och pessimistiska uppskattningar avviker avsevärt mellan olika aktiviteter. I detta fall kommer användningen av intervall och deras sannolikheter att återspegla spridningen och konfidensnivån hos de underliggande uppskattningarna.
Slutsats
Skattningen av aktiviteter med avseende på deras tids- och kostnadskrav är avgörande för planeringen och schemaläggningen av projekt och aktiviteter. I många projekt finns det inte tillgång till mer exakta uppskattningar, t.ex. parametriska uppskattningar som bygger på statistiska korrelationer av jämförbara projekt i det förflutna. Trepunktsmetoden för uppskattning är ett bra sätt att bearbeta och balansera uppskattningar uppifrån och ner eller från sakkunniga i sådana situationer.
PERT-fördelningen är förmodligen den mest exakta metoden för att sammanställa de värsta, bästa och mest sannolika fallen till en enda siffra (förväntat värde) eller ett intervall av värden. Tack vare användningen av standardavvikelsen tar den hänsyn till både de inneboende osäkerheterna och den potentiella spridningen av uppskattningar.
Detta kan vara anledningen till att PERT fortfarande är en vanlig metod för uppskattning och schemaläggning av projekt, trots att den har funnits i några decennier och redan kunde ha använts av våra mor- och farföräldrar (om de hade varit projektledare).
