Applicazione del teorema di Buckingham Pi

Prossimo: Importanza dei numeri non dimensionali Su: Teorema di Buckingham Pi Precedente: Teorema di Buckingham Pi

Applicazione del teorema di Buckingham Pi

Il teorema che abbiamo enunciato è molto generale, ma non è assolutamente limitato alla meccanica dei fluidi. È usato in campi diversificati come la botanica e le scienze sociali e sono stati scritti libri e volumi su questo argomento. Ma non abbiamo bisogno di molta teoria per poterla applicare. Ciò che considereremo è una procedura per usare il teorema e arrivare a numeri non dimensionali per un dato flusso.

1. Listare tutte le variabili che governano il processo. Queste variabili dovrebbero essere indipendenti l’una dall’altra. Per esempio, non si dovrebbe scegliere la densità, la gravità e il peso specifico. Densità e peso specifico dovrebbero bastare. Per il nostro problema abbiamo F, D, V, e . Abbiamo n = 5.
2. Marcare le variabili ripetitive. Nel nostro caso queste sono D, V e facendo k = 3.
3. Decidere quanti sono i numeri non dimensionali. Per il nostro caso abbiamo n – k = 2. Il nostro problema ha 2 numeri non dimensionali, e .
4. Definire i numeri non dimensionali raggruppando le variabili in n – k gruppi in modo che ogni gruppo abbia tutte le variabili ripetitive e una variabile non ripetitiva. Così per il nostro problema abbiamo

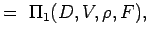
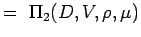
   		(5.2)
   Let
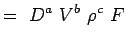
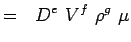
   		(5.3)

5. Ora esprimiamo ogni variabile in termini delle sue dimensioni. Usiamo il sistema MLT secondo il quale le variabili per i nostri problemi hanno le seguenti dimensioni.
   

   Variabile	Dimensioni
   F, Forza	M L / T2 o M L T-2
   D, Diametro:	L
   V, Velocità	L/T o LT-1
   , Densità:	M/L3 o ML-3
   , Viscosità	ML-1T-1

   Sostituendo queste dimensioni in Eqn. 5.2, abbiamo

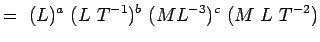
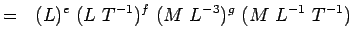
   		(5.4)
   Or
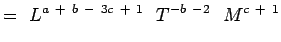
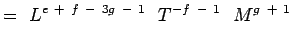
   		(5.5)

   Notando che e sono non dimensionali abbiamo,

   a + b – 3c + 1 = 0; -b – 2 = 0, c + 1 = 0
   e + f – 3g – 1 = 0; -f – 1 = 0;g + 1 = 0	(5.6)

   Solvendo le equazioni si ottiene,

   a = -2, b = -2, c = -1
   e = -1, f = -1, g = -1	(5.7)

   Ora i nostri numeri non dimensionali diventano,

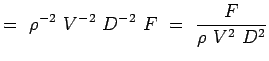
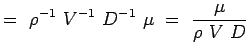
   		(5.8)

Così abbiamo trovato i numeri non-dimensionali per il flusso di interesse, cioè la resistenza intorno ad un cilindro circolare. La relazione funzionale tra i due numeri può essere espressa come

Ma si noti che la forma del termine che abbiamo derivato è un po’ diversa da quella che abbiamo assunto all’inizio. Il lato destro dell’equazione è in realtà l’inverso del numero di Reynolds! Questo indica lo svantaggio dell’analisi che la forma funzionale esatta tra i numeri non può essere ottenuta. Qualsiasi coefficiente o indice ottenuto non può essere determinato da questa analisi. Questo dovrebbe essere determinato dalla sperimentazione o da calcoli. Ma poiché i numeri non sono dimensionali possiamo scrivere

Prossimo: Importanza dei numeri non dimensionali Su: Teorema di Buckingham Pi Precedente: Teorema di Buckingham Pi

(c) Aerospace, Mechanical & Mechatronic Engg. 2005
Università di Sydney