La deviazione standard è un numero che ci dice
in che misura un insieme di numeri sono distanti tra loro.Una deviazione standard può variare da 0 a infinito. Una deviazione standard di 0 significa che una lista di numeri sono tutti uguali – non sono affatto distanti tra loro.
Deviazione standard – Esempio
Cinque candidati hanno fatto un test del QI come parte di una domanda di lavoro. I loro punteggi su tre componenti del QI sono mostrati qui sotto.
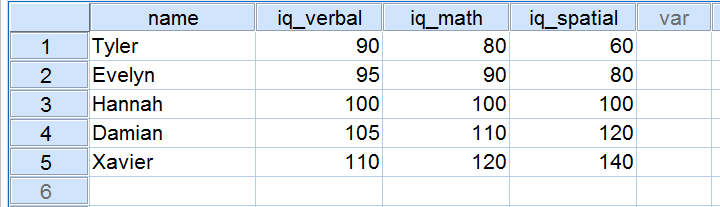
Ora, diamo un’occhiata da vicino ai punteggi sulle 3 componenti del QI. Notate che tutti e tre hanno una media di 100 sui nostri 5 candidati. Tuttavia, i punteggi di iq_verbal sono più vicini di quelli di iq_math. Inoltre, i punteggi su iq_spatial sono più distanti di quelli sulle prime due componenti. La misura precisa in cui un certo numero di punteggi sono distanti può essere espressa come un numero. Questo numero è noto come deviazione standard.
Deviazione standard – Risultati
Nella vita reale, ovviamente non ispezioniamo visivamente i punteggi grezzi per vedere quanto sono distanti. Invece, avremo semplicemente un software che li calcola per noi (ne parleremo più avanti). La tabella qui sotto mostra le deviazioni standard e alcune altre statistiche per i nostri dati del QI. Notate che le deviazioni standard confermano il modello che abbiamo visto nei dati grezzi.
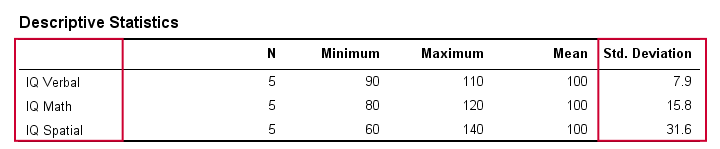
Deviazione standard e istogramma
Destra, rendiamo le cose un po’ più visive. La figura qui sotto mostra le deviazioni standard e gli istogrammi per i nostri punteggi del QI. Si noti che ogni barra rappresenta il punteggio di 1 candidato su 1 componente del QI. Ancora una volta, vediamo che le deviazioni standard indicano la misura in cui i punteggi sono distanti tra loro.
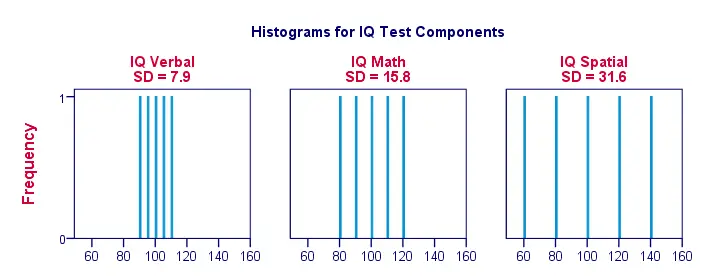
Deviazione standard – Altri istogrammi
Quando visualizziamo i dati su solo una manciata di osservazioni come nella figura precedente, vediamo facilmente un quadro chiaro. Per un esempio più realistico, presentiamo di seguito gli istogrammi per 1.000 osservazioni. È importante notare che questi istogrammi hanno scale identiche; per ogni istogramma, un centimetro sull’asse delle x corrisponde a circa 40 ‘punti di componenti del QI’.
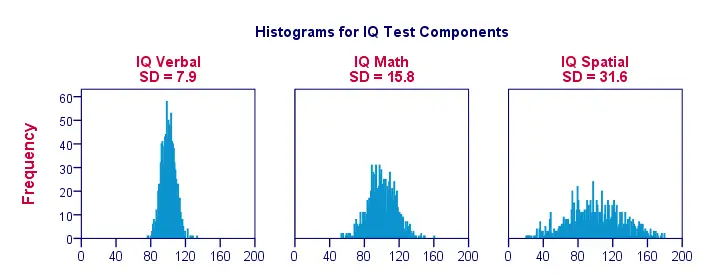
Nota come gli istogrammi permettono una stima approssimativa delle deviazioni standard. Gli istogrammi “più larghi” indicano deviazioni standard più grandi; i punteggi (asse delle x) sono più distanti tra loro. Poiché tutti gli istogrammi hanno aree di superficie identiche (corrispondenti a 1.000 osservazioni), deviazioni standard più alte sono anche associate a istogrammi più ‘bassi’.
Deviazione standard – Formula della popolazione
Come fa il tuo software a calcolare le deviazioni standard? Bene, la formula di base è
$$sigma = \sqrt{frac{\somma(X – \mu)^2}{N}}$$
dove
- (X\) denota ogni numero separato;
- (\mu\) indica la media su tutti i numeri e
- (\sum\) indica una somma.
In parole, la deviazione standard è la radice quadrata della differenza media al quadrato tra ogni singolo numero e la media di questi numeri.
Importante, questa formula presuppone che i vostri dati contengano l’intera popolazione di interesse (da qui “formula della popolazione”). Se i tuoi dati contengono solo un campione della tua popolazione di riferimento, vedi sotto.
Formula della popolazione – Software
Puoi usare questa formula in Google sheets, OpenOffice ed Excel digitando =STDEVP(...) in una cella. Specificate i numeri su cui volete la deviazione standard tra le parentesi e premete Invio. La figura qui sotto illustra l’idea.
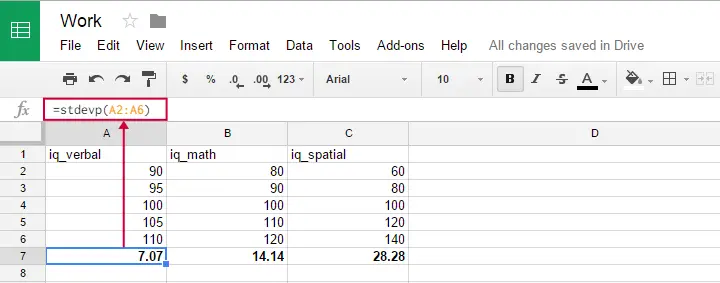
Purtroppo, la formula della deviazione standard della popolazione non sembra esistere in SPSS.
Deviazione standard – Formula del campione
Ora qualcosa di impegnativo: se i vostri dati sono (approssimativamente) un semplice campione casuale da una popolazione (molto) più grande, allora la formula precedente sottostimerà sistematicamente la deviazione standard in questa popolazione. Uno stimatore imparziale per la deviazione standard della popolazione si ottiene usando
$$S_x = \sqrt{\frac{\somma(X – \overline{X})^2}{N -1}}$
Per quanto riguarda i calcoli, la grande differenza con la prima formula è che noi dividiamo per \(n -1\) invece di \(n\). Dividendo per un numero più piccolo si ottiene un risultato (leggermente) più grande. Questo compensa precisamente la suddetta sottostima. Per campioni di grandi dimensioni, tuttavia, le due formule hanno risultati praticamente identici.
In GoogleSheets, Open Office e MS Excel, la funzione STDEV utilizza questa seconda formula. È anche la (unica) formula di deviazione standard implementata in SPSS.
Deviazione standard e varianza
Un secondo numero che esprime quanto lontano si trova un insieme di numeri è la varianza. La varianza è la deviazione standard al quadrato. Questo implica che, analogamente alla deviazione standard, la varianza ha una popolazione così come una formula campione.
In linea di principio, è imbarazzante che due diverse statistiche esprimano fondamentalmente la stessa proprietà di un insieme di numeri. Perché non scartiamo la varianza a favore della deviazione standard (o al contrario)? La risposta di base è che la deviazione standard ha proprietà più desiderabili in alcune situazioni e la varianza in altre.
