Alcuni anni fa, Scott Fortmann-Roe ha scritto un grande saggio intitolato “Capire il Bias-Variance Tradeoff.”
Quando la scienza dei dati si trasforma in una professione accettata con il suo set di strumenti, procedure, flussi di lavoro, ecc, spesso sembra che ci sia meno attenzione ai processi statistici a favore degli aspetti più eccitanti (vedere qui e qui per un paio di discussioni di esempio).
Definizioni concettuali
Mentre questo servirà come panoramica del saggio di Scott, che potrete leggere per ulteriori dettagli e approfondimenti matematici, inizieremo con le definizioni testuali di Fortmann-Roe che sono centrali per il pezzo:
Errore dovuto al bias: L’errore dovuto al bias è preso come la differenza tra la previsione attesa (o media) del nostro modello e il valore corretto che stiamo cercando di prevedere. Naturalmente avete solo un modello, quindi parlare di valori di predizione attesi o medi potrebbe sembrare un po’ strano. Tuttavia, immaginate di poter ripetere l’intero processo di costruzione del modello più di una volta: ogni volta raccogliete nuovi dati ed eseguite una nuova analisi creando un nuovo modello. A causa della casualità nei set di dati sottostanti, i modelli risultanti avranno una gamma di previsioni. La distorsione misura quanto in generale le previsioni di questi modelli siano lontane dal valore corretto.
Errore dovuto alla varianza: L’errore dovuto alla varianza è preso come la variabilità della previsione di un modello per un dato punto di dati. Di nuovo, immaginate di poter ripetere l’intero processo di costruzione del modello più volte. La varianza è quanto le previsioni per un dato punto variano tra diverse realizzazioni del modello.
In sostanza, il bias è quanto le previsioni di un modello sono lontane dalla correttezza, mentre la varianza è il grado in cui queste previsioni variano tra le iterazioni del modello.
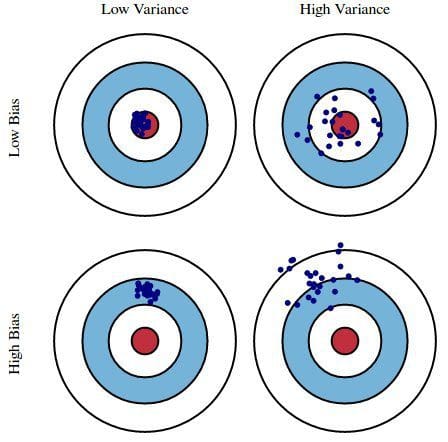
Fig. 1: Illustrazione grafica di bias e varianza
Da Understanding the Bias-Variance Tradeoff, di Scott Fortmann-Roe.
Discussione
Utilizzando un semplice e imperfetto sondaggio per le elezioni presidenziali come esempio, gli errori nel sondaggio vengono spiegati attraverso le lenti gemelle della distorsione e della varianza: la selezione dei partecipanti al sondaggio da un elenco telefonico è una fonte di distorsione; una piccola dimensione del campione è una fonte di varianza; la minimizzazione dell’errore totale del modello si basa sul bilanciamento degli errori di distorsione e varianza.
Fortmann-Roe continua a discutere questi problemi in relazione a un singolo algoritmo: k-Nearest Neighbor. Fornisce poi alcune questioni chiave a cui pensare quando si gestiscono bias e varianza, comprese le tecniche di ricampionamento, le proprietà asintotiche degli algoritmi e il loro effetto sugli errori di bias e varianza, e la lotta contro le proprie assunzioni nei confronti sia dei dati che della loro modellazione.
Il saggio finisce sostenendo che, nel loro cuore, questi 2 concetti sono strettamente legati sia all’over- che al under-fitting. A mio parere, questo è il punto più importante:
Come sempre più parametri vengono aggiunti a un modello, la complessità del modello aumenta e la varianza diventa la nostra preoccupazione principale mentre la distorsione diminuisce costantemente. Per esempio, più termini polinomiali vengono aggiunti a una regressione lineare, maggiore sarà la complessità del modello risultante. In altre parole, il bias ha una derivata di primo ordine negativa in risposta alla complessità del modello, mentre la varianza ha una pendenza positiva.

Fig. 2: Bias e varianza che contribuiscono all’errore totale
Da Understanding the Bias-Variance Tradeoff, di Scott Fortmann-Roe.
Fortmann-Roe termina la sezione sull’over- e under-fitting indicando un altro dei suoi grandi saggi (Accurately Measuring Model Prediction Error), e poi passando alla raccomandazione altamente condivisibile che “le misure basate sul ricampionamento come la convalida incrociata dovrebbero essere preferite alle misure teoriche come il criterio di informazione di Aikake”.
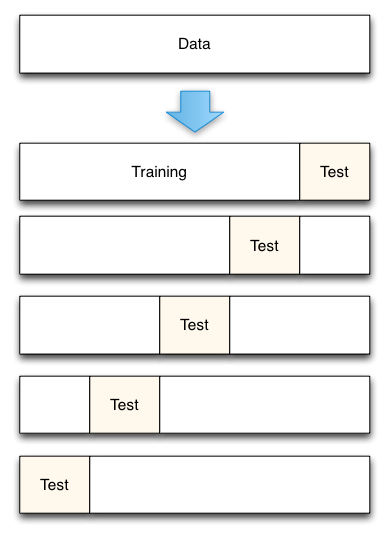
Fig. 3: 5-Fold cross-validation data split
Da Accurately Measuring Model Prediction Error, di Scott Fortmann-Roe.
Ovviamente, con la convalida incrociata, il numero di pieghe da usare (convalida incrociata k, giusto?), il valore di k è una decisione importante. Più basso è il valore, maggiore è la distorsione nelle stime di errore e minore è la varianza. Al contrario, quando k è impostato uguale al numero di istanze, la stima dell’errore è molto bassa in bias ma ha la possibilità di un’alta varianza. Il compromesso bias-varianza è chiaramente importante da capire anche per il più routinario dei metodi di valutazione statistica, come la convalida incrociata di k.
Purtroppo, anche la convalida incrociata sembra, a volte, aver perso il suo fascino nell’era moderna della scienza dei dati, ma questa è una discussione per un altro momento.
Consiglio di leggere l’intero saggio di Scott Fortmann-Roe sul tradeoff bias-varianza, così come il suo pezzo sulla misurazione dell’errore di previsione del modello.
Relati:
- Grandi dati, codici biblici e Bonferroni
- La scienza dei dati della selezione delle variabili: Una rassegna
- Insiemi di dati su algoritmi
