Questa è talvolta chiamata la teoria delle maree “statiche”, una teoria che emerse per la prima volta nei famosi Principia di Isaac Newton. Avendo identificato le forze che producono le maree, Newton, e altri che lo seguirono, concepirono un ipotetico oceano globale in equilibrio statico con queste forze – un equilibrio che richiedeva uno sferoide d’acqua apulato che coprisse la terra. “Prolato” significa che la sfera in questione è stata allungata lungo una linea che unisce due poli; non i poli geografici in questo caso, ma i poli in linea con il corpo celeste (luna o sole) causando la deformazione dell’ipotetica sfera oceanica. Dando un’altra occhiata alla grafica che illustra le forze di trazione nel modulo precedente, si può facilmente immaginare l’acqua che converge su questi poli per produrre due “rigonfiamenti di marea” gemelli – termini che sono ancora molto popolari nei libri di testo moderni.
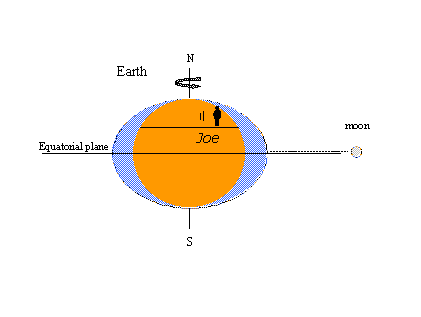
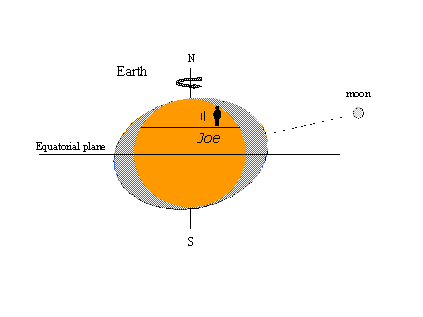
La ragione della popolarità della teoria dell’equilibrio – il concetto di rigonfiamenti di marea almeno – è che è facile spiegare alcuni fenomeni di marea ben noti con le immagini. In quella a sinistra in basso, un osservatore immaginario di nome Joe ruota con la terra e incontra i rigonfiamenti statici sotto forma di alte maree; ogni volta che la luna attraversa il meridiano locale di Joe, egli assiste all’alta marea. E’ di nuovo alta marea dodici ore lunari dopo, quando la luna attraversa il meridiano opposto dall’altra parte della terra. Due alte e due basse maree si verificano in un giorno lunare che dura 24 ore e 50 minuti in tempo di orologio (solare). Nella figura a destra, la luna ha progredito nella sua orbita intorno alla terra in una posizione a nord dell’equatore (declinazione nord). I rigonfiamenti statici si muovono per rimanere in linea con la luna e ora Joe incontra una disuguaglianza diurna nelle alte maree (alte maree successive di altezza disuguale). La massima declinazione lunare, a nord o a sud dell’equatore, produce le maree tropicali; le maree che si verificano quando la luna è sull’equatore sono chiamate maree equatoriali; le maree tropicali-equatoriali si ripetono due volte in un intervallo di 27 1/3 giorni – il mese tropico copre un ciclo completo nella declinazione lunare. Tutte queste osservazioni sono coerenti con la teoria dell’equilibrio.
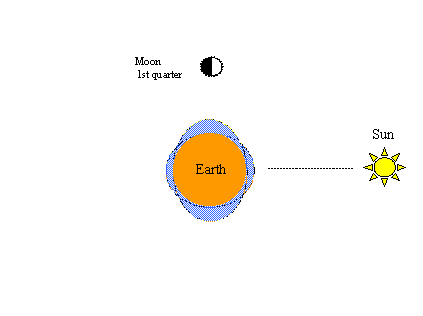
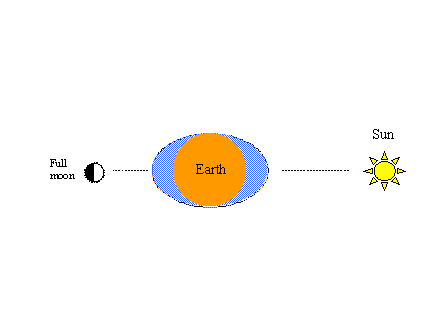
Un altro fenomeno facile da dimostrare in questo modo è il ben noto ciclo primavera-nove. La gravità solare produce anche un paio di rigonfiamenti di marea nell’oceano ipotetico. Quando le forze di trazione del sole e della luna sono in linea, le maree primaverili di maggiore portata (massimi più alti e minimi più bassi) risultano come mostrato nella figura a sinistra qui sotto. Come nelle figure precedenti, quando la luna completa un altro mezzo ciclo nella sua orbita – questa volta dalla luna piena alla luna nuova – le maree primaverili si verificheranno di nuovo.
La figura qui sotto a destra illustra la parte neap del ciclo primavera-neap; cioè, quando la luna è nel primo quarto (o il terzo quarto) di quel ciclo, le forze di trazione lunari e solari sono completamente fuori linea, tendendo a contrastarsi a vicenda, e le maree neap di minore portata (alti più bassi e bassi più alti) risultano. Due cicli primavera-neap (due primavere e due neaps) sono completati in 29 giorni e mezzo, lo stesso periodo di tempo richiesto alla luna per completare un’orbita completa della terra rispetto al sole.
Altri aspetti della marea osservata in accordo con la teoria dell’equilibrio includono il ciclo perigeo-apogeo. Questo deriva dal fatto che l’orbita della luna intorno alla terra descrive un’ellisse piuttosto che un cerchio. Le maree perigee di maggiore portata si verificano al perigeo lunare, quando la luna è più vicina alla terra, e le maree apogee di minore portata si verificano all’apogeo lunare, quando la luna è più lontana dalla terra nella sua orbita ellittica. Il ciclo perigeo-apogeo impiega circa 27 giorni e mezzo per completarsi.
Anche se la teoria dell’equilibrio fa un ottimo lavoro per spiegare i fenomeni ciclici delle maree e i periodi di ricorrenza associati a molti di essi, è un esempio di un modello di comportamento ideale – qualcosa che funziona per lo scopo previsto anche se non può aderire alla verità in tutte le circostanze. Non dobbiamo cercare molto lontano questi casi. La terra è solo parzialmente coperta dalle sue acque, le masse terrestri impediscono a qualsiasi cosa che assomigli ad un’onda di viaggiare completamente intorno ad essa, e le osservazioni delle maree reali mostrano che esse non rispondono istantaneamente alle forze che producono le maree della luna e del sole come richiede la teoria.
