Link state routing è una tecnica in cui ogni router condivide la conoscenza del suo quartiere con ogni altro router nell’internetwork.
Le tre chiavi per capire l’algoritmo Link State Routing:
- Conoscenza del quartiere: invece di inviare la sua tabella di routing, un router invia solo le informazioni sul suo quartiere. Un router trasmette le sue identità e il costo dei collegamenti direttamente collegati agli altri router.
- Flooding: Ogni router invia le informazioni ad ogni altro router dell’internetwork tranne i suoi vicini. Questo processo è noto come Flooding. Ogni router che riceve il pacchetto invia le copie a tutti i suoi vicini. Infine, ogni router riceve una copia delle stesse informazioni.
- Condivisione delle informazioni: Un router invia le informazioni ad ogni altro router solo quando si verifica un cambiamento nelle informazioni.
Link State Routing ha due fasi:
Reliable Flooding
- Stato iniziale: Ogni nodo conosce il costo dei suoi vicini.
- Stato finale: Ogni nodo conosce l’intero grafico.
Calcolo del percorso
Ogni nodo usa l’algoritmo di Dijkstra sul grafico per calcolare i percorsi ottimali per tutti i nodi.
- L’algoritmo Link state routing è anche conosciuto come algoritmo di Dijkstra che è usato per trovare il percorso più breve da un nodo ad ogni altro nodo della rete.
- L’algoritmo di Dijkstra è iterativo, e ha la proprietà che dopo la kesima iterazione dell’algoritmo, i percorsi meno costosi sono ben noti per k nodi di destinazione.
Descriviamo alcune notazioni:
- c( i , j): Costo del collegamento dal nodo i al nodo j. Se i nodi i e j non sono direttamente collegati, allora c(i , j) = ∞.
- D(v): Definisce il costo del percorso dal codice sorgente alla destinazione v che ha attualmente il minor costo.
- P(v): Definisce il nodo precedente (vicino di v) insieme al percorso meno costoso corrente dalla sorgente a v.
- N: È il numero totale di nodi disponibili nella rete.
Algoritmo
InitializationN = {A} // A is a root node.for all nodes vif v adjacent to Athen D(v) = c(A,v)else D(v) = infinityloopfind w not in N such that D(w) is a minimum.Add w to NUpdate D(v) for all v adjacent to w and not in N:D(v) = min(D(v) , D(w) + c(w,v))Until all nodes in N
Nell’algoritmo precedente, un passo di inizializzazione è seguito dal loop. Il numero di volte che il ciclo viene eseguito è uguale al numero totale di nodi disponibili nella rete.
Comprendiamo attraverso un esempio:
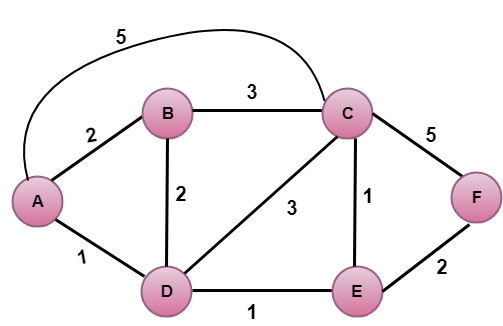
Nella figura sopra, il vertice sorgente è A.
Passo 1:
Il primo passo è un passo di inizializzazione. Il percorso di minor costo attualmente noto da A ai suoi vicini diretti, B, C, D sono rispettivamente 2,5,1. Il costo da A a B è impostato a 2, da A a D è impostato a 1 e da A a C è impostato a 5. Il costo da A a E e F sono impostati su infinito perché non sono direttamente collegati ad A.
| Step | N | D(B),P(B) | D(C),P(C) | D(D),P(D) | D(E),P(E) | D(F),P(F) |
|---|---|---|---|---|---|---|
| 1 | A | 2,A | 5,A | 1,A | ∞ | ∞ |
Step 2:
Nella tabella precedente, osserviamo che il vertice D contiene il percorso meno costoso nel passo 1. Pertanto, è aggiunto in N. Ora, abbiamo bisogno di determinare un percorso di minor costo attraverso il vertice D.
a) Calcolo del percorso più breve da A a B
b) Calcolo del percorso più breve da A a C
c) Calcolo del percorso più breve da A a E
Nota: Il vertice D non ha un collegamento diretto al vertice E. Pertanto, il valore di D(F) è infinito.
| Step | N | D(B),P(B) | D(C),P(C) | D(D),P(D) | D(E),P(E) | D(F),P(F) |
|---|---|---|---|---|---|---|
| 1 | A | 2,A | 5,A | 1,A | ∞ | ∞ |
| 2 | AD | 2,A | 4,D | 2,D | ∞ |
Step 3:
Nella tabella precedente, osserviamo che sia E che B hanno il percorso meno costoso nel passo 2. Consideriamo il vertice E. Ora, determiniamo il percorso meno costoso dei restanti vertici attraverso E.
a) Calcolo del percorso più breve da A a B.
b) Calcolo del percorso più breve da A a C.
c) Calcolo del percorso più breve da A a F.
| Step | N | D(B),P(B) | D(C),P(C) | D(D),P(D) | D(E),P(E) | D(F),P(F) |
|---|---|---|---|---|---|---|
| 1 | A | 2,A | 5,A | 1,A | ∞ | ∞ |
| 2 | AD | 2,A | 4,D | 2,D | ∞ | |
| 3 | ADE | 2,A | 3,E | 4,E |
Step 4:
Nella tabella precedente, osserviamo che il vertice B ha il percorso meno costoso nel passo 3. Pertanto, viene aggiunto in N. Ora, determiniamo il percorso meno costoso dei restanti vertici attraverso B.
a) Calcolando il percorso più breve da A a C.
b) Calcolando il percorso più breve da A a F.
| Step | N | D(B),P(B) | D(C),P(C) | D(D),P(D) | D(E),P(E) | D(F),P(F) |
|---|---|---|---|---|---|---|
| 1 | A | 2,A | 5,A | 1,A | ∞ | ∞ |
| 2 | AD | 2,A | 4,D | 2,D | ∞ | |
| 3 | ADE | 2,A | 3,E | 4,E | ||
| 4 | ADEB | 3,E | 4,E |
Step 5:
Nella tabella precedente, osserviamo che il vertice C ha il percorso meno costoso nel passo 4. Pertanto, viene aggiunto in N. Ora, determiniamo il percorso meno costoso dei restanti vertici attraverso C.
a) Calcolo del percorso più breve da A a F.
| Step | N | D(B),P(B) | D(C),P(C) | D(D),P(D) | D(E),P(E) | D(F),P(F) | |
|---|---|---|---|---|---|---|---|
| 1 | A | 2,A | 5,A | 1,A | ∞ | ∞ | |
| 2 | AD | 2,A | 4,D | 2,D | ∞ | ||
| 3 | ADE | 2,A | 3,E | 4,E | |||
| 4 | ADEB | 3,E | 4,E | ||||
| 5 | ADEBC | 4,E |
Tabella finale:
| Step | N | D(B),P(B) | D(C),P(C) | D(D),P(D) | D(E),P(E) | D(F),P(F) |
|---|---|---|---|---|---|---|
| 1 | A | 2,A | 5,A | 1,A | ∞ | ∞ |
| 2 | AD | 2,A | 4,D | 2,D | ∞ | |
| 3 | ADE | 2,A | 3,E | 4,E | ||
| 4 | ADEB | 3,E | 4,E | |||
| 5 | ADEBC | 4,E | ||||
| 6 | ADEBCF |
Svantaggio:
Si crea un traffico pesante nel Line state routing a causa del Flooding. Il Flooding può causare un looping infinito, questo problema può essere risolto utilizzando il campo Time-to-leave
.
