Introduzione:
La similarità del coseno è usata per determinare la similarità tra documenti o vettori. Matematicamente, misura il coseno dell’angolo tra due vettori proiettati in uno spazio multidimensionale. Ci sono altre tecniche di misurazione della somiglianza come la distanza euclidea o la distanza di Manhattan disponibili, ma qui ci concentreremo sulla somiglianza del coseno e sulla distanza del coseno.
La relazione tra somiglianza coseno e distanza coseno può essere definita come segue.
- La somiglianza diminuisce quando la distanza tra due vettori aumenta

2. La somiglianza aumenta quando la distanza tra due vettori diminuisce.

Similitudine coseno e distanza coseno:
Similitudine coseno dice che per trovare la similitudine tra due punti o vettori dobbiamo trovare l’angolo tra loro.
La formula per trovare la somiglianza e la distanza del coseno è la seguente:


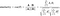
Qui A=Punto P1,B=Punto P2 (nel nostro esempio)
Vediamo i vari valori di Cos Θ per capire la similarità del coseno e la distanza del coseno tra due punti dati (vettori) P1 & P2 considerando due assi X e Y.
Nell’immagine che segue ci sono dei casi.
Caso 1: Quando l’angolo tra i punti P1 & P2 è di 45 gradi, allora
cosintonia_similarità= Cos 45 = 0.525
Caso 2: Quando due punti P1 & P2 sono lontani tra loro e l’angolo tra i punti è di 90 gradi allora
cosine_similarity= Cos 90 = 0
Caso 3: Quando due punti P1 & P2 sono molto vicini e si trovano sullo stesso asse l’uno all’altro e l’angolo tra i punti è 0 gradi allora
cosine_similarity= Cos 0 = 1

L’immagine seguente ha tre casi.
Caso 4: Quando i punti P1 & P2 si trovano uno di fronte all’altro e l’angolo tra i punti è 180 gradi allora
cosine_similarity= Cos 180 = -1
Caso 5: Quando l’angolo tra i punti P1 & P2 è 270 gradi allora
cosine_similarity= Cos 270 = 0
Caso 6: Quando l’angolo tra i punti P1 & P2 è di 360 gradi allora
cosine_similarity= Cos 360 = 1

Passiamo questi valori di ogni angolo discusso sopra e vediamo la distanza Coseno tra due punti.
1 – Cosine_Similarity=Cosine_Distance
Caso 1: Quando Cos 45 Degree
Sostituiamo i valori nella formula di sopra .
1-0.525= Coseno_Distanza
0.475 =Cosine_Distance
Caso 2: Quando Cos 90 Grado
1-0= Cosine_Distance
1 =Cosine_Distance
Caso 3: Quando Cos 0 Grado
1-1= Cosine_Distance
0 =Cosine_Distance
Caso 4: Quando Cos 180 Grado
1-(-1)= Cosine_Distance
2 =Cosine_Distance
Caso 5: Quando Cos 270 Grado
1-0= Cosine_Distance
1 =Cosine_Distance
Caso 6: Quando Cos 360 gradi
1-1= Cosine_Distance
0 =Cosine_Distance
Possiamo chiaramente vedere che quando la distanza è minore la somiglianza è maggiore (i punti sono vicini l’uno all’altro) e la distanza è maggiore, due punti sono dissimili (lontani l’uno dall’altro)
Similitudine del coseno e distanza del coseno sono molto usati nei sistemi di raccomandazione per raccomandare prodotti agli utenti in base ai loro gusti e antipatie.
Pochi esempi in cui questo è usato sono siti web come Amazon, Flipkart per raccomandare articoli ai clienti per un’esperienza personalizzata, valutazione e raccomandazione di film ecc.
Conclusione: Spero che a questo punto abbiate una chiara comprensione della matematica dietro il calcolo della somiglianza del coseno e della distanza del coseno e il suo utilizzo.
Spero che vi piaccia il mio articolo, per favore battete il Clap 👏 (50 volte) per motivarmi a scrivere ulteriormente.
Vuoi connetterti :
Linked In : https://www.linkedin.com/in/anjani-kumar-9b969a39/
Se ti piacciono i miei post qui su Medium e desideri che io continui a fare questo lavoro, considera di sostenermi su patreon
