Om breuken op te tellen (of af te trekken) is het nodig dat de noemers van de breuken gelijk zijn.
Gelijke noemers
Als de noemers gelijk zijn, wordt de som van de breuken berekend door de tellers op te tellen en de noemer te behouden.
Voorbeeld:
Laten we 4/7 en 3/7 optellen:
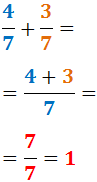 Op dezelfde manier wordt het aftrekken van breuken met gelijke noemers berekend door de tellers van elkaar af te trekken en de noemer te behouden.
Op dezelfde manier wordt het aftrekken van breuken met gelijke noemers berekend door de tellers van elkaar af te trekken en de noemer te behouden.
Voorbeeld:
We trekken 4/7 en 3/7 van elkaar af:
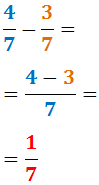
Verschillende noemers
Wanneer de noemers verschillend zijn, moeten we een beetje opereren om de breuken te veranderen in gelijkwaardige breuken, zodat ze dezelfde noemer hebben.
Laten we de procedure uitleggen voor het berekenen van de som
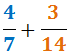
1. We berekenen het kleinste gemene veelvoud van de noemers:
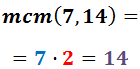
2. In de noemer van elke breuk schrijven we het verkregen kleinste gemene veelvoud:
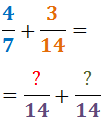
3. In de teller van elke breuk schrijven we het resultaat van de deling van het kleinste gemene veelvoud (de nieuwe noemer) door de oorspronkelijke noemer en de vermenigvuldiging met de oorspronkelijke teller: De oorspronkelijke noemer van de eerste breuk was 7 en de oorspronkelijke teller was 4:
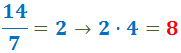
De oorspronkelijke noemer van de tweede breuk was 14 en de oorspronkelijke teller was 3:
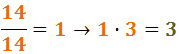
Dus hebben we de som van twee breuken met gelijke noemer:
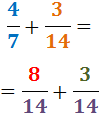
4. We tellen de breuken op:
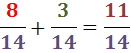
Om af te trekken volgen we dezelfde stappen, maar aan het eind, in plaats van de breuken op te tellen, trekken we ze af.
Fracties bronnen:
- Begrip van breuk
- Vereenvoudigen van breuken
- Equivalente breuken (1)
- Equivalente breuken (2)
- Tellen en aftrekken van breuken
- Vermenigvuldigen en delen. breuken
- Fracties die decimale getallen genereren
- Gemengde breuken
- Problemen met percentages
- Interactieve breukoefeningen
- Operaties met breuken
