Inleiding :
Cosinegelijkenis wordt gebruikt om de gelijkenis tussen documenten of vectoren te bepalen. Mathematisch meet het de cosinus van de hoek tussen twee vectoren geprojecteerd in een multidimensionale ruimte.Er zijn andere technieken voor het meten van overeenkomst beschikbaar, zoals de Euclidische afstand of de Manhattan-afstand, maar wij zullen ons hier richten op de Cosinus-gelijkenis en de Cosinus-afstand.
De relatie tussen cosinusgelijkheid en cosinusafstand kan als volgt worden gedefinieerd.
- Gelijkenis neemt af wanneer de afstand tussen twee vectoren toeneemt

2. Gelijkenis neemt toe wanneer de afstand tussen twee vectoren afneemt.

Cosine Gelijkenis en Cosine Afstand:
Cosine Gelijkenis zegt dat om de gelijkenis tussen twee punten of vectoren te vinden we de hoek tussen hen moeten vinden.
De formule om de cosinusgelijkenis en de cosinusafstand te vinden is de volgende:


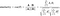
Hier A=Punt P1,B=Punt P2 (in ons voorbeeld)
Laten we de verschillende waarden van Cos Θ zien om de cosinusgelijkenis en cosinusafstand tussen twee gegevenspunten (vectoren) P1 & P2 te begrijpen, rekening houdend met twee assen X en Y.
Onderstaande afbeelding bevat gevallen.
Geval 1: Wanneer de hoek tussen de punten P1 & P2 45 graden is, dan
cosine_similarity= Cos 45 = 0.525
Voorbeeld 2: Wanneer twee punten P1 & P2 ver van elkaar verwijderd zijn en de hoek tussen de punten is 90 graden dan
cosine_similarity= Cos 90 = 0
Voorbeeld 3: Wanneer twee punten P1 & P2 zeer dicht bij elkaar liggen en op dezelfde as ten opzichte van elkaar liggen en de hoek tussen de punten is 0 graden dan
cosine_similarity= Cos 0 = 1

Afbeelding hieronder heeft de volgende drie gevallen.
Geval 4: Wanneer de punten P1 & P2 tegenover elkaar liggen en de hoek tussen de punten 180 graden is, dan
cosine_similarity= Cos 180 = -1
Geval 5: Wanneer de hoek tussen de punten P1 & P2 270 graden is, dan
cosine_similarity= Cos 270 = 0
Geval 6: Wanneer de hoek tussen de punten P1 & P2 360 graden is dan
cosine_similarity= Cos 360 = 1

Laten we deze waarden van elke hierboven besproken hoek doorlopen en de Cosine-afstand tussen twee punten bekijken.
1 – Cosine_Similarity=Cosine_Distance
Geval 1: Wanneer Cos 45 Graden
Laten we de waarden in bovenstaande formule vervangen .
1-0.525=Cosinus_afstand
0.475 =Cosine_Distance
Case 2: When Cos 90 Degree
1-0= Cosine_Distance
1 =Cosine_Distance
Case 3: When Cos 0 Degree
1-1= Cosine_Distance
0 =Cosine_Distance
Case 4: Wanneer Cos 180 Degree
1-(-1)= Cosine_Distance
2 =Cosine_Distance
Case 5: Wanneer Cos 270 Degree
1-0= Cosine_Distance
1 =Cosine_Distance
Case 6: Wanneer Cos 360 Degree
1-1= Cosine_Distance
0 =Cosine_Distance
We kunnen duidelijk zien dat wanneer de afstand kleiner is, de gelijkenis groter is (punten zijn dicht bij elkaar) en de afstand groter is, twee punten ongelijk zijn (ver weg van elkaar)
Cosine Gelijkenis en Cosine Afstand wordt veel gebruikt in aanbevelingssystemen om producten aan de gebruikers aan te bevelen op basis van hun sympathieën en antipathieën.
Weinig voorbeelden waar dit wordt gebruikt zijn websites zoals Amazon, Flipkart aan te bevelen items aan klanten voor gepersonaliseerde ervaring, Films rating en aanbeveling etc.
Conclusie : Ik hoop dat je nu een goed begrip hebt van de wiskunde achter de berekening van cosine similarity en Cosine Distance en het gebruik ervan.
Hoop dat je mijn artikel leuk vindt.Sla alsjeblieft op Clap 👏(50 keer) om me te motiveren om verder te schrijven.
Wil je in contact komen :
Linked In : https://www.linkedin.com/in/anjani-kumar-9b969a39/
Als mijn berichten hier op Medium je bevallen en als je wilt dat ik dit werk blijf doen, kun je overwegen me te steunen op patreon
