Dit wordt soms de theorie van de “statische” getijden genoemd, een theorie die voor het eerst naar voren kwam in de beroemde Principia van Isaac Newton. Nadat hij de getijden producerende krachten had geïdentificeerd, bedachten Newton, en anderen die na hem kwamen, een hypothetische wereldoceaan in statisch evenwicht met deze krachten – een evenwicht dat een geprolateerde sferoïde van water opleverde die de aarde bedekte. “Prolate’ betekent dat de bol in kwestie is uitgerekt langs een lijn die twee polen verbindt; niet de geografische polen in dit geval, maar de polen in het verlengde van het hemellichaam (maan of zon) waardoor de hypothetische oceaanbol vervormt. Als we nog eens naar de grafiek kijken die de trekkrachten in de vorige module illustreert, kunnen we ons gemakkelijk voorstellen dat het water op deze polen samenkomt en twee “getijdenbulten” produceert – een term die nog steeds erg populair is in moderne leerboeken.
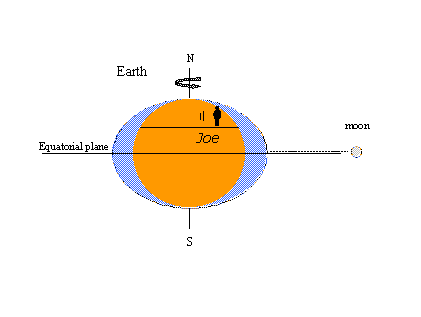
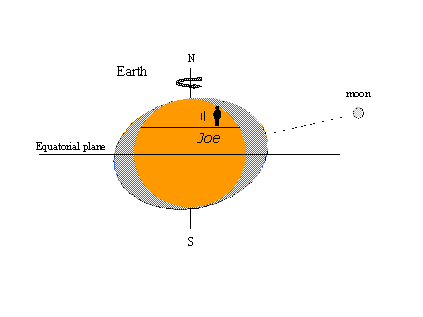
De reden voor de populariteit van de evenwichtstheorie – althans het concept van de getijdenbulten – is dat het gemakkelijk is om bepaalde bekende getijdenverschijnselen met plaatjes te verklaren. In het plaatje linksonder draait een denkbeeldige waarnemer genaamd Joe met de aarde mee en komt de statische uitstulpingen tegen in de vorm van hoogwater. Telkens wanneer de maan Joe’s plaatselijke meridiaan kruist, is hij getuige van hoogwater. Twaalf maanuren later, als de maan de tegengestelde meridiaan aan de andere kant van de aarde kruist, is het weer hoogtij. Twee hoogten en twee laagten komen voor op één zonnedag die 24 uur en 50 minuten duurt in horloge (zonne) tijd. In de figuur rechts is de maan in haar baan om de aarde gevorderd tot een positie ten noorden van de evenaar (noorderdeclinatie). De statische uitstulpingen bewegen zich in het verlengde van de maan en nu krijgt Joe te maken met een dagelijkse ongelijkheid in het hoogwater (opeenvolgende hoogwaters van ongelijke hoogte). De maximale stand van de maan, ten noorden of ten zuiden van de evenaar, veroorzaakt tropische getijden; getijden die optreden wanneer de maan op de evenaar staat, worden equatoriale getijden genoemd. Tropische-equatoriale getijden komen tweemaal voor in een interval van 27 1/3 dagen – de tropische maand die één volledige cyclus in maansdeclinatie omvat. Al deze waarnemingen zijn in overeenstemming met de evenwichtstheorie.
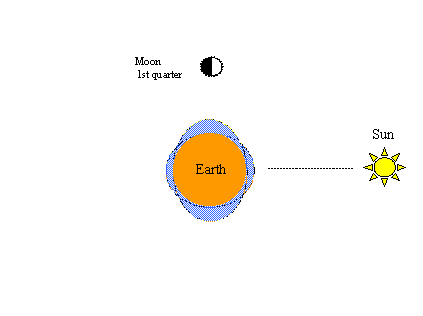
Een ander verschijnsel dat op deze manier gemakkelijk kan worden aangetoond is de bekende lente-nap-cyclus. De zwaartekracht van de zon veroorzaakt ook een paar getijdebulten in de hypothetische oceaan. Wanneer de trekkrachten van de zon en de maan op één lijn staan, ontstaan springtij met een groter bereik (hogere hoogten en lagere laagten), zoals te zien is in de figuur linksonder. Zoals in de vorige figuren, wanneer de maan een andere halve cyclus in zijn baan voltooit – dit keer van volle naar nieuwe maan – zullen opnieuw springtijgen optreden.
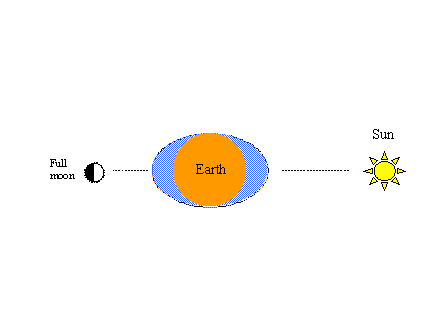
De figuur rechtsonder illustreert het doodtij-gedeelte van de lente-nieuwe-maancyclus; d.w.z. wanneer de maan in het eerste kwartier (of het derde kwartier) van die cyclus is, zijn de trekkrachten van de maan en de zon volledig uit het lood, neigen ertoe elkaar tegen te werken en resulteren de doodtij-getijden van geringer bereik (lagere hoogten en hogere laagten). Twee lente-najaarscycli (twee keer lente en twee keer doodtij) worden voltooid in 29 ½ dag, dezelfde tijd die de maan nodig heeft om een volledige baan om de aarde ten opzichte van de zon af te leggen.
Andere aspecten van het waargenomen getij die in overeenstemming zijn met de evenwichtstheorie zijn onder andere de perigean-apogean cyclus. Deze vloeit voort uit het feit dat de baan van de maan om de aarde een ellips beschrijft in plaats van een cirkel. Perigean getijden van grotere reikwijdte treden op bij maanperigeum, wanneer de maan het dichtst bij de aarde is, en apogean getijden van kleinere reikwijdte treden op bij maanapogeum, wanneer de maan het verst van de aarde verwijderd is in haar elliptische baan. De perigean-apogean cyclus neemt ongeveer 27 ½ dag in beslag.
Hoewel de evenwichtstheorie een uitstekend werk levert in het verklaren van cyclische getijdenverschijnselen en de herhalingsperioden die met veel van deze verschijnselen gepaard gaan, is het een voorbeeld van een model van ideaal gedrag – iets dat werkt voor het beoogde doel, hoewel het misschien niet in alle omstandigheden aan de waarheid beantwoordt. We hoeven niet ver te zoeken naar die gevallen. De aarde wordt slechts gedeeltelijk bedekt door haar wateren, landmassa’s verhinderen dat iets wat op een vloed lijkt zich volledig om haar heen kan verplaatsen, en waarnemingen van echte getijden tonen aan dat zij niet onmiddellijk reageren op de getij-producerende krachten van de maan en de zon zoals de theorie voorschrijft.
