Enkele jaren geleden schreef Scott Fortmann-Roe een geweldig essay getiteld “Understanding the Bias-Variance Tradeoff.”
Naarmate data science zich ontwikkelt tot een geaccepteerd beroep met zijn eigen set tools, procedures, workflows, etc., lijkt er vaak minder aandacht te zijn voor statistische processen ten gunste van de meer opwindende aspecten (zie hier en hier voor een paar voorbeelddiscussies).
Conceptuele definities
Hoewel dit zal dienen als een overzicht van Scott’s essay, dat u kunt lezen voor verdere details en wiskundige inzichten, zullen we beginnen met Fortmann-Roe’s woordelijke definities die centraal staan in het stuk:
Fout door bias: De fout door bias wordt opgevat als het verschil tussen de verwachte (of gemiddelde) voorspelling van ons model en de juiste waarde die we proberen te voorspellen. Natuurlijk hebt u slechts één model, zodat het een beetje vreemd kan lijken om over verwachte of gemiddelde voorspellingswaarden te spreken. Stel u echter voor dat u het hele proces van modelvorming meer dan eens zou kunnen herhalen: telkens verzamelt u nieuwe gegevens en voert u een nieuwe analyse uit, waardoor een nieuw model ontstaat. Door de willekeurigheid van de onderliggende gegevensverzamelingen zullen de resulterende modellen een reeks voorspellingen hebben. De bias meet hoe ver de voorspellingen van deze modellen in het algemeen van de juiste waarde afliggen.
Fout door variantie: De variatiefout wordt opgevat als de variabiliteit van een modelvoorspelling voor een gegeven gegeven gegevenspunt. Nogmaals, stel je voor dat je het hele modelbouwproces meerdere malen kunt herhalen. De variantie is hoeveel de voorspellingen voor een gegeven punt variëren tussen verschillende realisaties van het model.
In wezen is bias hoe ver de voorspellingen van een model verwijderd zijn van juistheid, terwijl variantie de mate is waarin deze voorspellingen variëren tussen model-iteraties.
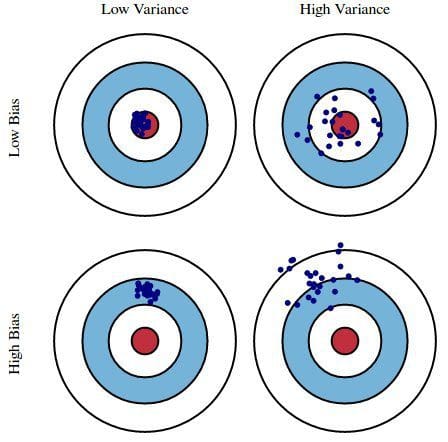
Fig. 1: Grafische illustratie van bias en variantie
Van Understanding the Bias-Variance Tradeoff, door Scott Fortmann-Roe.
Discussie
Gebaseerd op een eenvoudige enquête over de presidentsverkiezingen met fouten als voorbeeld, worden fouten in de enquête verklaard door de dubbele bril van bias en variantie: het selecteren van deelnemers aan de enquête uit een telefoonboek is een bron van bias; een kleine steekproefgrootte is een bron van variantie; het minimaliseren van de totale modelfout berust op het in evenwicht brengen van bias- en variantiefouten.
Fortmann-Roe bespreekt deze kwesties vervolgens in relatie tot één algoritme: k-Nearest Neighbor. Vervolgens geeft hij een aantal kernpunten waarover moet worden nagedacht bij het beheersen van bias en variantie, waaronder herbemonsteringstechnieken, asymptotische eigenschappen van algoritmen en hun effect op bias en variantiefouten, en het bestrijden van aannames ten aanzien van zowel de gegevens als de modellering ervan.
Het essay eindigt met de stelling dat deze twee concepten in hun kern nauw samenhangen met zowel over- als under-fitting. Naar mijn mening is dit het belangrijkste punt:
Naarmate er meer en meer parameters aan een model worden toegevoegd, neemt de complexiteit van het model toe en wordt variantie onze grootste zorg, terwijl bias gestaag afneemt. Naarmate bijvoorbeeld meer polynomiale termen aan een lineaire regressie worden toegevoegd, zal de complexiteit van het resulterende model toenemen. Met andere woorden, de bias heeft een negatieve eerste-orde-afgeleide als reactie op de complexiteit van het model, terwijl de variantie een positieve helling heeft.

Fig. 2: Bias en variantie dragen bij tot de totale fout
Van Understanding the Bias-Variance Tradeoff, door Scott Fortmann-Roe.
Fortmann-Roe eindigt het hoofdstuk over over- en onder-fitting met een verwijzing naar een ander groot essay van hem (Accurately Measuring Model Prediction Error), en gaat dan verder met de zeer instemmende aanbeveling dat “op resampling gebaseerde maatstaven zoals kruisvalidatie de voorkeur verdienen boven theoretische maatstaven zoals Aikake’s Informatie Criteria.”
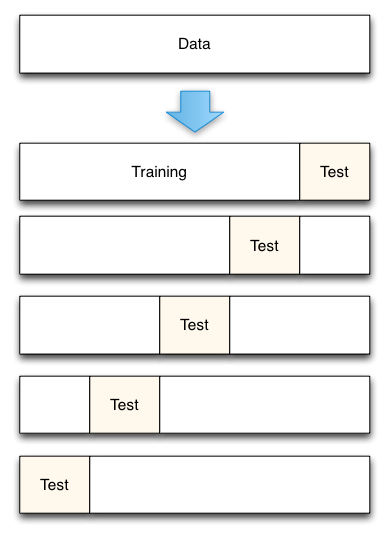
Fig. 3: 5-voudige kruisvalidatie datasplitsing
Van Accurately Measuring Model Prediction Error, door Scott Fortmann-Roe.
Natuurlijk is bij kruisvalidatie het aantal te gebruiken vouwen (k-voudige kruisvalidatie, toch?), de waarde van k een belangrijke beslissing. Hoe lager de waarde, hoe groter de bias in de foutschattingen en hoe kleiner de variantie. Omgekeerd, wanneer k gelijk wordt gesteld aan het aantal instanties, is de foutenschatting dan zeer laag in bias maar heeft de mogelijkheid van hoge variantie. De bias-variantie tradeoff is duidelijk belangrijk om te begrijpen voor zelfs de meest routineuze van statistische evaluatiemethoden, zoals k-voudige kruisvalidatie.
Helaas lijkt kruisvalidatie ook, soms, zijn allure te hebben verloren in het moderne tijdperk van data science, maar dat is een discussie voor een andere keer.
Ik raad aan het volledige bias-variantie tradeoff essay van Scott Fortmann-Roe te lezen, evenals zijn stuk over het meten van modelvoorspellingsfout.
Gerelateerd:
- Big Data, Bible Codes, and Bonferroni
- Data Science of Variable Selection: A Review
- Datasets Over Algorithms
